Курсовая работа: Статистический анализ выборочных совокупностей

Если значения признака х₁ , х₂ , …., х_k имеют соответственно частоты n₁ , n₂ , …..n_k , причем n₁ +n₂ +……+n_k =n, то

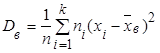. (18)

Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:

. (19)

Начальный эмпирический момент порядка s статистического распределения определяют по формуле

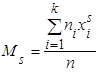, (20)

где x_i – наблюдаемое значение признака, n_i – частота наблюдаемого значения признака, n – объем выборки.

Начальный эмпирический момент первого порядка равен выборочной средней .

Центральный эмпирический момент порядка sстатистического распределения определяют по формуле

.

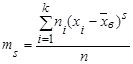Центральный эмпирический момент второго порядка равен выборочной дисперсии .

Коэффициент асимметрии статистического распределения определяется по формуле

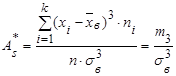. (22)

Эксцесс статистического распределения определяется по формуле

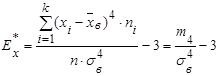. (23)

Относительной характеристикой рассеивания случайной величины выступает коэффициент вариации V, который вычисляется как отношение среднего квадратического отклонения и выборочной средней по формуле

. (24)

Метод моментов

Метод моментов – это определение неизвестных параметров статистического распределения путем приравнивания теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же порядка.

Для нахождения параметра λ показательного распределения необходимо приравнять начальный момент первого порядка показательного распределения начальному моменту первого порядка эмпирического распределения:

(25)

Для нахождения параметров а и σ нормального распределения необходимо:

1) приравнять начальный момент первого порядка нормального распределения к начальному моменту первого порядка эмпирического распределения:

; (26)

2) центральный момент второго порядка нормального распределения к центральному моменту второго порядка эмпирического распределения:

. (27)

Для нахождения параметров a и bравномерного распределениянеобходимо:

1) приравнять начальный момент первого порядка равномерного распределения к начальному моменту первого порядка эмпирического распределения:

;