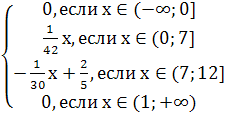Курсовая работа: Статистическое изучение выборочных данных экономических показателей

Пусть распределение случайной величины Х задаётся плотностью , имеющей вид:

,

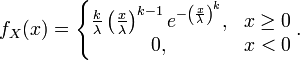где λ и k параметры распределения

Тогда говорят, что X имеет распределение Вейбулла.

Функция распределения

F(x)=1-

Математическое ожидание

M(x)=λГ

Дисперсия

D(x)=

2) Задача

Пассажир может уехать на любом из двух маршрутов автобусов.Закон времени ожидания прихода этих автобусов задается графикомплотности распределения вероятности случайной величины X.

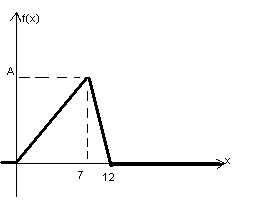
Требуется найти:

1) параметр А,

2) плотность распределенияf(x),

3) функцию распределения F(x) (найти аналитическую формулу и построить график),

4) числовые характеристики: математическое ожидание M(x), дисперсию D(x) и среднее квадратическое отклонение (х),

5) вероятность того, что во время ожидания пассажиром автобуса составит от 3,5 до 6 (вероятность попадания величины в интервал (3,5;6))

Решение

1)

f(x)=

Найдем А по условию нормировки:

+A

6А=1

А

2)

f(x)