Курсовая работа: Статистическое изучение выборочных данных экономических показателей
3. Корреляция величин
3.1 Корреляция величин
Корреляция — зависимость между случайными величинами, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной зависимости корреляции, как правило, рассматривается тогда, когда одна из величин зависит не только от данной другой, но и от ряда случайных факторов. Зависимость между двумя случайными событиями проявляется в том, что условная вероятность одного из них при наступлении другого отличается от безусловной вероятности. Аналогично, влияние одной случайной величины на другую характеризуется условными распределениями одной из них при фиксированных значениях другой.
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными (возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин). Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент корреляции может быть отрицательным; положительная корреляция в таких условиях — корреляция, при которой увеличение одной переменной связано с увеличением другой переменной, при этом коэффициент корреляции может быть положительным.
3.2 Задача
Совместный закон распределения суммы дивидендов, выплачиваемых по привилегированной и обыкновенной акциям некоторой компании, задается следующей таблицей
| 0 | 1 | 2 | |
| 2 | |||
| 4 | |||
![]()
1) Построить маргинальные законы распределения случайных величин X и Y.
![]() ) =
) =![]()
![]() )=
)=![]()
![]()
Проверка: ![]()
| Y | 0 | 1 | 2 |
| p |
X: ![]() )=
)=![]()
![]() )=
)=![]()
Проверка: ![]()
| X | 2 | 4 |
| p |
2) Вычислить числовые характеристики: математические ожидания ![]() и
и ![]() , дисперсии
, дисперсии ![]() и
и ![]() , среднеквадратические отклонения
, среднеквадратические отклонения ![]() и
и ![]()
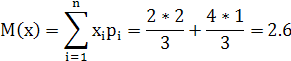
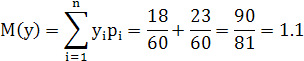
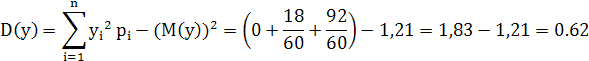
![]()
![]()
![]()
3) Условные вероятности составляющих X и Y соответственно вычисляются по соответствующим формулам:
P(![]()
![]()
![]()
| X | 2 | 4 |
| 0,75 | 0.44 |
![]()
![]()
![]()
| X | 0 | 1 | 2 |
| 0.3 | 0.325 | 0.375 |