Математика / Курсовая работа: Теорема Силова

Курсовая работа: Теорема Силова

Таким образом, группа G состоит из 6 элементов: G =.

Докажем, что c 2 = e . Действительно, очевидно, что c 2 ≠ c , ac , a 2 c .

Если было бы c 2 = a (или c 2 = a 2 ), то выполняется следующие c 3 = c 2 c = ac = d ≠ e , противоречие с условием, что все элементы группы G имеют либо второй или третий порядок (следовательно, c 3 = c 2 c = a 2 c = f ≠ e ). Таким образом, ни c 2 , ни c 3 не равно e , что противоречит условию. Значит c 2 = e .

Покажем также, что d 2 = f 2 = e , то есть c произвольный элемент не входящий в подгруппу , то d 2 ≠ a , a 2 ( f 2 ≠ a , a 2 ) . Не сложно видеть, что d 2 =( ac ) 2 ≠ c (иначе d = ac = b ), d 2 =( ac ) 2 ≠ ac , d 2 =( ac ) 2 ≠ a 2 c = f (иначе f = a 2 c = b ). Таким образом, d 2 =( ac ) 2 = e и более того, a 3 = c 2 =( ac )( ac )= e .

Известно, что симметрическую группу подстановок S 3 , можно задать двумя образующими и тремя определяющими соотношениями. Следующим образом S 3 = где в качестве x можно взять подстановку , а в качестве y : .

Следовательно, мы можем утверждать, что . Таким образом, если G группа и , то G изоморфна либо ℤ6 , либо S 3 .

Далее выпишем все элементы группы A 4 и построим таблицу умножения элементов.

Все 4!=24 перестановки из четырёх символов 1, 2, 3, 4 расположим в таком порядке, чтобы каждая последующая перестановка получалась от предыдущей с помощью одной транспозиции (перемены мест двух символов).

Начнём с перестановки 1, 2, 3, 4. Итак,
.

Так как всякая транспозиция меняет четность перестановки, то в полученном ряду все перестановки, взятые через одну, являются четными (они подчеркнуты).

Теперь уже легко составить все искомые четные подстановки достаточно в каждой из них в качестве первой строки записать перестановку (1234), а в качестве второй строки одну из найденных четных перестановок. Итак,

A4 =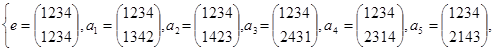

.

Строим таблицу умножения.

Таблица 1

e a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11
e e a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11
a1 a1 a2 e a4 a5 a3 a7 a8 a6 a10 a11 a9
a2 a2 e a1 a5 a3 a4 a8 a6 a7 a11 a9 a10
a3 a3 a7 a9 a11 a8 a1 a2 a5 a10 a6 a4 e
a4 a4 a8 a10 a9 a6 a2 е a3 a11 a7 a5 a1
a5 a5 a6 a11 a10 a7 e a1 a4 a9 a8 a3 a2
a6 a6 a11 a5 a7 e a10 a4 a9 a1 a3 a2 a8
a7 a7 a9 a3 a8 a1 a11 a5 a10 a2 a4 e a6
a8 a8 a10 a4 a6 a2 a9 a3 a11 e a5 a1 a7
a9 a9 a3 a7 a1 a11 a8 a10 a2 a5 e a6 a4
a10 a10 a4 a8 a2 a9 a6 a11 e a3 a1 a7 a5
a11 a11 a5 a6 e a10 a7 a9 a1 a4 a2 a8 a3

Из таблицы 1 видим, что элементами второго порядка будут:

и, кроме того, эти элементы попарно перестоновочны. Заметим, что в A 4 нет элементов шестого порядка. Действительно, a 1 = a 1 a 1 a 1 = e элемент третьего порядка,

a 2 = a 2 a 2 a 2 = e элемент третьего порядка,

a 3 = a 3 a 3 a 3 = e элемент третьего порядка,

a 4 = a 4 a 4 a 4 = e элемент третьего порядка,

a 6 = a 6 a 6 a 6 = e элемент третьего порядка,

a 7 = a 7 a 7 a 7 = e элемент третьего порядка,

a 10 = a 10 a 10 a 10 = e элемент третьего порядка,

a 11 = a 11 a 11 a 11 = e элемент третьего порядка.

Из приведенных вычислений следует, что в группе A 4 нет элемента шестого порядка. Следовательно, искомая подгруппа A 4 не изоморфна циклической группе ℤ6 .

Заметим также, что в группе подстановок S 3 существуют элементы второго порядка, но они не перестановочны. В самом деле, выпишем все элементы симметрической группы.

S3 =.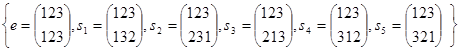

Построим их таблицу умножения.

Таблица 2

e s1 s2 s3 s4 s5
е e s1 s2 s3 s4 s5
s10 s1 e s3 s2 s5 s4
s2 s2 s5 s4 s1 е s3
s3 s3 s4 s5 e s1 s2
s4 s4 s3 e s5 s2 s1
s5 s5 s2 s1 s4 s3 e

Несложно видеть, что элементы s 1 , s 3 , и s 5 будут элементами второго порядка, но они как видно из таблицы 2 не перестановочны, и, следовательно, никакая подгруппа группы A 4 не изоморфна группе S 3 . Утверждение доказано.

К-во Просмотров: 378
Бесплатно скачать Курсовая работа: Теорема Силова