Курсовая работа: Теория столкновений

к плотности потока падающих частиц

Заметим, что, обсуждая сечение, мы имеем в виду расстояниях r, большие не только по сравнению с a, радиусом действия потенциала, но и с дебройлевской длиной волны λ.

От дифференциального УШ (1.1) и граничного условия (1.2) удобно перейти к интегральному уравнению

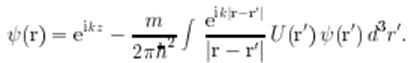(1.3)

Такой переход можно обосновать известными из электродинамики результатами (см. Ландау Л.Д., Лифшиц Е.М. Теория поля (М.: Наука, 1988, § 64). Действительно, волновое уравнение

при гармонической зависимости от времени потенциалов и плотностей зарядов

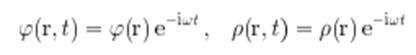
имеет вид

(1.4)

аналогичный (1.1) с заменой

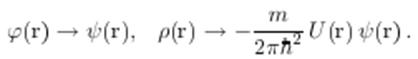
Решение же уравнения (20.4) в форме запаздывающих потенциалов таково:

что соответствует суперпозиции сферических волн , расходящихся из центров , в которых сосредоточены заряды .

При r >> a соотношение (1.3) приводится к виду (1.2). Действительно, при этом

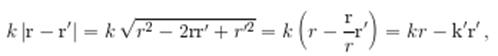
так что

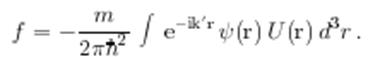(1.5)

2. Борновское приближение. Формула Резерфорда. Атомный форм-фактор

2.1 Борновское приближение

Рассматриваем потенциал как возмущение. Для получения амплитуды рассеяния в первом порядке по потенциалу взаимодействия, подставим в (1.5) невозмущенную волновую функцию

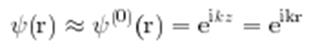
и получим

2.2 Критерий применимости

, что дает для сферически симметричного потенциала условие