Курсовая работа: Теория столкновений

При частицы не сталкиваются с шаром, .

При частицы полностью поглощаются, . Строго говоря, эти утверждения справедливы лишь для , но область не дает большого вклада в сечение. Таким образом,

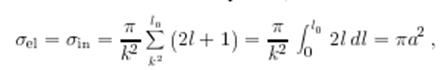
то есть полное сечение вдвое больше классического

Амплитуда упругого рассеяния велика лишь в области малых углов

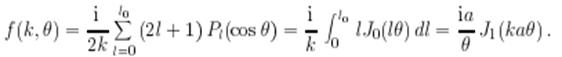
Поэтому

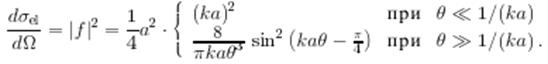
3.5 Упругое рассеяние быстрых частиц на идеально отражающем шаре

Пусть радиус шара a и ka >> 1. Полное сечение определяет число частиц, выбывших из начального пучка. В классике это сечение связано лишь с прямым столкновением с мишенью. С учетом волновых свойств частиц их выбывание из пучка, то есть изменение начального импульса, связано также с дифракцией.

Как и в предыдущем случае

При решение УШ для радиальной волновой функции имеет вид при r < a и

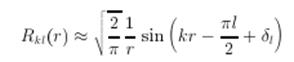
Сшивка при r = a дает . Для нахождения полного сечения используем оптическую теорему

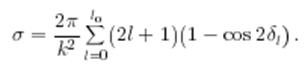
Слагаемые, содержащие , быстро осциллируют при изменении , и поэтому их вкладом в сумму можно пренебречь. В итоге получаем , что вдвое превышает классическое сечение В данном случае отличие от классического результата связано с наличием помимо квазиклассического рассеяния, обусловленного углами θ >> 1/ka, дифракционного рассеяния на малые углы

Чтобы увидеть это, представим амплитуду рассеяния

в виде двух слагаемых совпадает с амплитудой рассеяния в предыдущем случае, а

Доказательство того факта, что (в полном соответствии с классическим изотропным рассеянием ) можно найти в задаче

Таким образом, вклады в полное сечение одинаковы, а вклад их интерференции пренебрежимо мал.

Для классических частиц дифракция практически ненаблюдаема. Так, для частицы с m ∼ 1 г, v ∼ 1 см/с углы дифракции на шаре радиуса a ∼ 1 см настолько малы, , что увидеть это рассеяние можно было бы лишь на расстояниях см.

3.6 Резонансное рассеяние

Перепишем асимптотическое выражение (при r →∞)