Курсовая работа: Теория вероятностей

Доверительные интервалы для ,, не накрывают значение равное нулю, следовательно, факторы ,, являются значимыми, а факторы ,, - незначимыми.

11. Оценка значимости факторов по доверительным интервалам

Исключив из уравнения регрессии незначимые факторы, приходим к следующему виду:

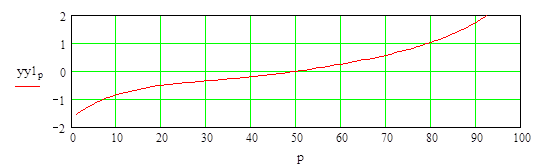
Таким образом, из графика видно, что при исключении из уравнения регрессии незначимых факторов график не изменился. Найдем доверительный интервал для остаточной дисперсии

при .

А доверительный интервал найдём из следующего двойного неравенства:

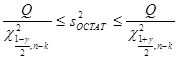
Таким образом, доверительный интервал для остаточной дисперсии есть:

Выводы

Таким образом, в данной курсовой работе были изучены методы обработки случайных выборок с нормальным законом распределения. Так же найдены оценки коэффициентов регрессии и построены доверительные интервалы. В последнем пункте работы были оценены значимости факторов по доверительным интервалам.