Курсовая работа: Теория вероятностей

Для (1) строим доверительные интервалы для математического ожидания (считая s2 известной и неизвестной) и дисперсии.

Считаем s2 известной.

Считаем s2 неизвестной.

Таким образом, при различных вариантах μmin, μmax имеют почти одинаковые значения.

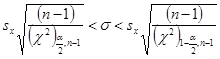
Подставляем табличные значения 24,7 и 5,01 в знаменатели подкоренного выражения и получаем, что

,

,

4. Построение доверительного интервала для коэффициента корреляции

Для (1), (2) строим доверительный интервал для коэффициента корреляции.

U = 1,96

Так как , то пусть , отсюда z = 0,693

То есть |z| ≤ 0,693.

Если z = –0,693 и z = 0,693, то получим доверительный интервал для коэффициента корреляции –0,6 < Rxy < 0,6.

5. Построение эмпирической интегральной функции распределения и теоретической (для нормального закона с оценками среднего и дисперсии)