Курсовая работа: Теория вероятностей

Построение эмпирических Fx(u), Fy(u) и теоретических интегральных функций распределения. В последних средние и с. к. о. Взяты равными вычисленным оценкам математического ожидания и с. к. о.

Пусть u = 0, 0.001…6, тогда

,

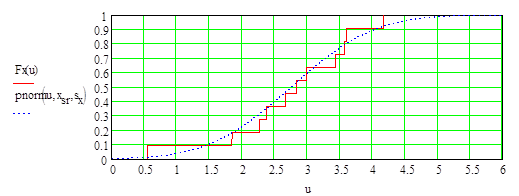
- - - - теоретическая функция распределения.

____ функция для нормального закона с оценками среднего и дисперсии.

6. Построение эмпирической кривой плотности распределения и теоретической

случайный выборка доверительный интервал

Для (1) построить эмпирическую кривую плотности распределения, разбив интервал (х(1),х(n)) на несколько подинтервалов. На этом же графике изобразить теоретическую кривую.

k*sigx - ширина интервалов разбиения, k - коэффициент шага разбиния. взято симметрично от среднего значения по 4 интервала

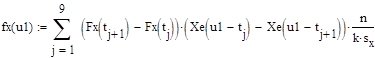
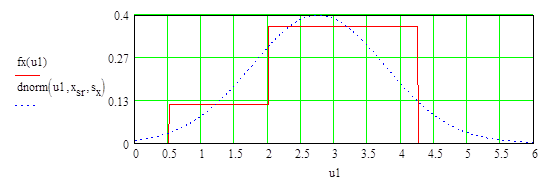
- - - - теоретическая функция плотности распределения.

____ эмпирическая кривая плотности распределения.

7. Проверка гипотезы о величине среднего (m), дисперсии (s2), о нормальном законе распределения (по c2 и по Колмогорову)

Проверка по критерию согласия Пирсона:

По данным выборки найдем теоретические частоты , затем, сравнивая их с наблюдаемыми частотами , рассмотрим статистику - случайная физическая величина, имеющая распределение с k степенями свободы. Если сумма , то выборочные данные согласуются с нормальным распределением и нет оснований отвергать нулевую гипотезу.

Определим с степенями свободы: