Курсовая работа: Топологические пространства

т.е. и – непустые дизъюнктные замкнутые множества. Но f (О ₁ ) f (О ₂ ) = Y , значит,

= f (О ₁ ) и = f (О ₂ ),

т.е. эти множества открыто-замкнутые. Это противоречит связности пространства Y.

Таким образом, предположение о несвязности топологического пространства Х неверно, а верно то, что требуется доказать. €

Другой связи между связностью пространств и связностью отображений может и не быть.

Рис. 2.

Рис. 1.

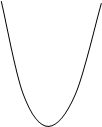
Примеры. ????? ??????????? f : X→ Y ??????????. ???? ???????????? Х ??????, ?? ? ??? ????? f (X ) ??????, ?? ??????????? f ?? ??????? ???? ???????. ? ??????, ????? f : R ? [0; + ¥], ? f (х ) = х ² ??? ?????? х Î R (???. 1). ????????? ???????????? ????? y Î (0; + ¥). ????? ???????????? ????? y ???????? ????? ???????? U = (a ; b ) Í (0; + ¥), ?????????? ??? ?????. ????? ??????

f ^–1 (U ) =

распадается на два непустых не