Курсовая работа: Цифровая система передачи информации с импульсно-кодовой модуляцией
В MathCad’е посчитаем значение вероятности ошибки
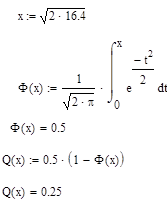
Таким образом, получается, что вероятность ошибки для данного канала связи 0.25
Рассчитаем, как нужно изменить энергию сигнала, чтобы в системах передачи с другими видами модуляции сохранялось такое же значение вероятности ошибки при когерентном приеме.
Для АМ системы с пассивной паузой вероятность ошибки рассчитывается по формуле:
Для ЧМ систем с ортогональными сигналами:
Для ФМ систем с противоположными сигналами:
Исходя из анализа значений вероятности ошибки для различных видов модуляции следует, что при переходе от системы с АМ к системе с ЧМ энергетический выигрыш по максимальной мощности равен 2, а при переходе к системе с ФМ – 4. Если же сравнение вести по средней мощности, то переход от АМ к ЧМ выигрыша не дает. Таким образом, максимальную потенциальную помехоустойчивость обеспечивает система с ФМ.
8. РАСЧЕТ ДЕКОДЕРА
Задачей декодера является исправление ошибок, которые могут возникать при передаче сигнала по каналу связи.
Построение проверочной матрицы Н: проверочная матрица может быть получена из порождающей матрицы кода. Матрица Н имеет n столбцов и n-k строк. Она связана с порождающей матрицей уравнениями:
![]()
где Т – символ транспонирования.
Для кода (7,4,3) проверочная матрица имеет вид:
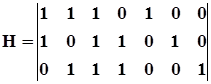 |
Если принятую кодовую комбинацию С умножить на порождающую матрицу Н, то в результате мы получим вектор синдрома (локатор ошибки) S,который однозначно связан с номером ошибочного символа: S = H*C. C есть вектор- столбец, содержащий n элементов, где n =7. Для синдромов, определяющих ошибку в конкретном разряде кода, составим таблицу.
|
Номер ошибки |
Синдром |
|
0 – нет ошибки |
000 |
|
1 |
110 |
|
2 |
101 |
|
3 |
111 |
|
4 |
011 |
|
5 |
100 |
|
К-во Просмотров: 642
Бесплатно скачать Курсовая работа: Цифровая система передачи информации с импульсно-кодовой модуляцией
|