Курсовая работа: Уменьшение оценки взаимной спектральной плотности стационарного случайного процесса

,

,

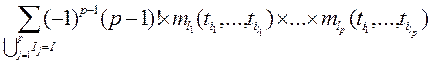где суммирование производится по всевозможным разбиениям множества

, , , , .

При

,

,

.

При

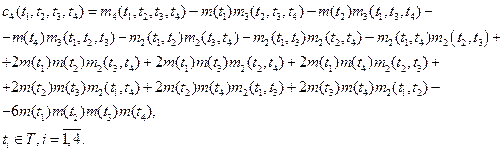
Спектральной плотностью случайного процесса , , называется функция вида

=, ,

при условии, что

Из определения видно, что спектральная плотность непрерывная, периодическая функция с периодом, равным по каждому из аргументов.

Семиинвариантной спектральной плотностью го порядка, , случайного процесса , , называется функция вида

=, ,

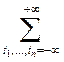
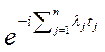при условии, что

.

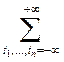
Теорема 1. Для смешанного семиинварианта го порядка, , случайного процесса справедливы представления

,.

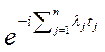
Пусть - случайный процесс, заданный на вероятностном пространстве , и

- мерная функция распределения, где

Случайный процесс называется стационарным в узком смысле (строго стационарным), если для любого натурального , любых и любого , такого что выполняется соотношение

где

Возьмем произвольное . Пусть , тогда