Курсовая работа: Уменьшение оценки взаимной спектральной плотности стационарного случайного процесса

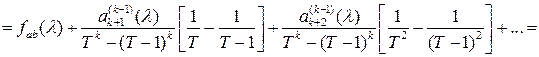
где

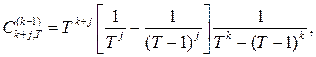
Следовательно, оценка является асимптотически несмещенной со смещением, убывающим как .

Найдем явный вид коэффициентов в представлении (2.4),

Видим, что

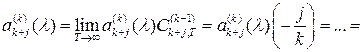
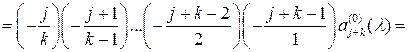
Таким образом, справедливо следующее утверждение.

Теорема 2.1 . Оценка взаимной спектральной плотности стационарного в широком смысле случайного процесса , задаваемая равенством (2.5), удовлетворяет соотношению

,

,

при условии, что справедливо соотношение (2.4) для

При нахождении моментов оценок спектральных плотностей вторых и высших порядков появляются функции вида

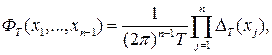(2.6)

где задаются соотношением

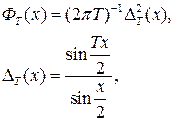
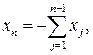
3. ОКНА ПРОСМОТРА ДАННЫХ

Чтобы выделить определенные характеристики спектральных оценок, нередко прибегают к сглаживанию значений на концах случайного временного ряда. Временное сглаживание представляет собой умножение ряда на «окно данных».

В соотношении (2.3) введена функция , называемая окном просмотра данных (множителем сходимости, коэффициентом сглаживания).

Функцию

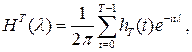(3.1)

называют частотным окном. Из соотношения (3.1) вытекает, что

Характерное поведение функции состоит в том, что она становится все более сконцентрированной в окрестности нуля при .