Курсовая работа: Уменьшение оценки взаимной спектральной плотности стационарного случайного процесса

s – целое число, - целая часть числа .

Статистика , называемая выборочной взаимной спектральной плотностью или периодограммой, задается соотношением

(2.3)

определено равенством (2.2).

Предположим, если оценка взаимной спектральной плотности , построенная по T наблюдениям, является асимптотически несмещенной, то математическое ожидание ее можно представить в виде

(2.4)

где некоторые действительные функции, не зависящие от T,

В качестве оценки взаимной спектральной плотности возьмем статистику

,

и исследуем первый момент построенной оценки.

Математическое ожидание построенной оценки будет следующее

Использовав соотношение (2.4), получим

где

Поскольку

следовательно, оценка является асимптотически несмещенной со смещением, убывающим как .

Так как равенство (2.4) справедливо и при , то, рассматривая оценку

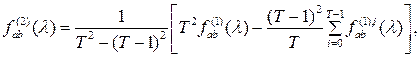
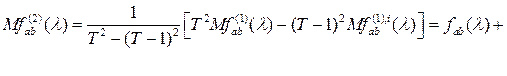
где

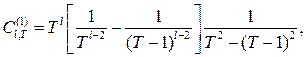
, то оценка является асимптотически несмещенной со смещением, убывающим на . Далее рассмотрим оценку

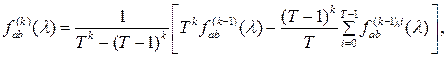(2.5)

Найдем математическое ожидание построенной оценки :