Курсовая работа: Уменьшение оценки взаимной спектральной плотности стационарного случайного процесса
В дальнейшем функцию, в правой части (1), будем обозначать
Используя определение стационарного в узком смысле СП 
, смешанный момент 
го порядка, 
, будем обозначать
Смешанный семиинвариант го порядка, , стационарного в узком смысле СП будем обозначать
Случайный процесс , называется стационарным в широком смысле , если 
и
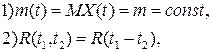
Замечание 1. Если , является стационарным в узком смысле СП и 
то , является стационарным в широком смысле, но не наоборот.
Спектральной плотностью стационарного случайного процесса 
, называется функция вида
,
при условии, что
Семиинвариантной спектральной плотностью 
- го порядка , , стационарного СП , называется функция вида
при условии, что
Для смешанного семиинварианта -го порядка, , стационарного СП 
справедливо следующее соотношение
.
Для 
эти соотношения примут вид
.
2. УМЕНЬШЕНИЕ СМЕЩЕНИЯ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
Рассмотрим действительный стационарный в широком смысле случайный процесс
,
, с математическим ожиданием 
, 
, взаимной ковариационной функцией 
, и взаимной спектральной плотностью 
.
Предположим, имеются Т последовательных, полученных через равные промежутки времени наблюдений 
за составляющей 
, рассматриваемого процесса 
. Как оценку взаимной спектральной плотности в точке 
рассмотрим статистику
(2.1)
где 
, - произвольная, не зависящая от наблюдений четная целочисленная функция, 
для 
, а