Курсовая работа: Уравнения и неравенства с модулем на централизованном тестировании

Пример Два тела начинают одновременно двигаться равномерно по прямым и , пересекающимися под прямым углом. Первое тело движется со скоростью 3 км/ч по прямой от точки к точке , находящейся на расстоянии 2 км от точки . Второе тело движется со скоростью 4 км/ч по прямой от точки к точке , находящейся на расстоянии 3 км от точки . Найти наименьшее расстояние (в км) между этими телами во время движения.

Решение. Через часов первое тело будет находится от точки на расстоянии км, а второе --- на расстоянии км. По теореме Пифагора расстояние между телами составит . км.

Ответ. км.

Пример Пункты и расположены на прямолинейной магистрали в 9 км друг от друга. Из пункта в направлении пункта выходит автомашина, двигающаяся равномерно со скоростью 40 км/ч. Одновременно из пункта в том же направлении с постоянным ускорением 32 км/ч выходит мотоцикл. Найти наибольшее расстояние между машиной и мотоциклом в течении первых двух часов движения.

Решение. Расстояние между автомобилем и мотоциклом через часов составит . .

Ответ. 16 км.

Пример Из пункта в пункт вышел пешеход. Не позже чем через 40 мин вслед за ним вышел второй. Известно, что в пункт один из них пришел раньше другого не менее, чем на 1 час. Если бы пешеходы вышли одновременно, то они бы пришли в пункт с интервалом не более чем в 20 мин. Определить, сколько времени требуется каждому пешеходу на путь от до , если скорость одного из них в 1,5 раза больше скорости другого.

Решение. Пусть и (мин) --- время, затраченное соответственно первым и вторым пешеходом на путь из в , и пусть второй пешеход вышел позже первого на минут. Рассмотри 2 возможности 1) и 2) . В случае имеем равенство и систему

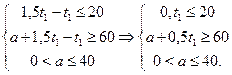
Из первого и третьего неравенства получим , учитывая второе условие получим, что , и это в свою очередь дает равенства и . Т.о. , , .

В случае имеем и сиcтему

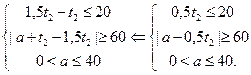
Но так как , то система не совместна, и, следовательно, случай 2 не может иметь места.

Ответ. , , .

Пример По расписанию автобус должен проходить путь , состоящий из отрезков , , длиной 5, 1, 4 км соответственно, за 1 час. При этом выезжая из пункта в 10 ч, он проходит пункт в 10 ч 10 мин, пункт в 10ч 34 мин. С какой скоростью должен ехать автобус, чтобы время за которое автобус проходит половину пути от до (со скоростью ), сложенное с суммой абсолютных величинотклонения от расписания при прохождении пунктов и , превышало абсолютную величину отклонения от расписания при прохождении пункта не более, чем на 28 мин.

Решение. Условие задачи приводит к системе

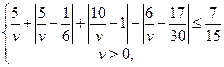
которая имеет единственное решение .

Ответ. 30 км/ч.

Пример Согласно расписанию катер проходит по реке, скорость течения которой 5 км/ч, путь из в длиной 15 км за 1 час. При этом выходя из пункта в 12ч, он прибывает в пункты и , отстоящие от на растояние 11 км и 13 км соответственно, в 12 ч 20 мин и в 12 ч 40 мин. Известно, что если бы катер двигался из в без остановок с постоянной скоростью (относительно воды), то сумма абсолютных величин отклонений от расписания прибытия в пункты , , не превышало бы уменьшенного на полчаса времени, необходимого катеру для прохождения 5 км со скоростью в стоячей воде. Какой из пунктов находится выше по течению: или ?

Решение. Рассмотрим 2 случая 1) пункт находится выше по течению 2) пункт находится ниже по течению.

В первом случае получаем систему

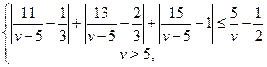
которая не имеет решения. Тогда выполняется второй случай.

Ответ. .

Пример Даны три квадратных трехчлена: , и . Докажите, что уравнение имеет не более восьми корней.

Решение. Каждый корень данного уравнения является корнем одного из квадратных трехчленов , , с некоторым набором знаков. Таких наборов 8, и все они дают действительно квадратные трехчлены, так как коэффициент при имеет вид , т.е. отличен от нуля. Однако двум противоположным наборам знаков соответствуют квадратные уравнения, имеющие одни и те же корни. Значит, все решения уравнения содержатся среди корней четырех квадратных уравнений. Следовательно, их не более восьми.

Пример Шабат Г.Б. Бесконечная последовательность чисел определяется условиями: , причем . Докажите, что последовательность, начиная с некоторого места, периодическая в том случае, если рационально.

Решение. Если , то . Действительно, . Если рациональное, то рациональное, причем со знаменателем не большим чем у . Действительно, пусть --- несократимая дробь. Тогда