Курсовая работа: Векторные многоугольники в физических задачах
![]() ,
, ![]() , (2.4 9)
, (2.4 9)
где ![]() . В силу закона сохранения импульса импульсы обеих частиц в Ц-системе остаются после столкновения равными по модулю и направленными в противоположные стороны, в силу закона сохранения энергии модули импульсов в Ц - системе при столкновении не меняются. Таким образом, в Ц-системе результат столкновения сводится лишь к повороту скоростей обеих частиц, причем после поворота скорости остаются направленными в противоположные стороны. Если единичный вектор
. В силу закона сохранения импульса импульсы обеих частиц в Ц-системе остаются после столкновения равными по модулю и направленными в противоположные стороны, в силу закона сохранения энергии модули импульсов в Ц - системе при столкновении не меняются. Таким образом, в Ц-системе результат столкновения сводится лишь к повороту скоростей обеих частиц, причем после поворота скорости остаются направленными в противоположные стороны. Если единичный вектор ![]() выражает направление скорости
выражает направление скорости![]() первой частицы после столкновения, то в Ц-системе.
первой частицы после столкновения, то в Ц-системе.
![]() ,
,![]() . (2.4 10)
. (2.4 10)
Чтобы вернуться к JI-системе, нужно к этим выражениям добавить скорость![]() центра масс:
центра масс:
 (2.4 11)
(2.4 11)
Этим исчерпываются сведения, которые можно получить из одних только законов сохранения импульса и энергии. Направление вектора ![]() зависит от условий взаимодействия частиц (от взаимного расположения во время столкновения и т.п.).
зависит от условий взаимодействия частиц (от взаимного расположения во время столкновения и т.п.).
Для геометрической интерпретации результатов перейдем опять к импульсам. Из (2.4 11) получим:
 (2.4 12)
(2.4 12)
где ![]() - приведенная масса частицы. Векторная диаграмма импульсов, соответствующая (2.4 12), приведена на рисунке 9. Здесь
- приведенная масса частицы. Векторная диаграмма импульсов, соответствующая (2.4 12), приведена на рисунке 9. Здесь
![]() ,
,![]() ,
,![]() .
.
При заданных ![]() и
и ![]() радиус окружности и положения точек А и В неизменны, а точка С может иметь любое положение на окружности.
радиус окружности и положения точек А и В неизменны, а точка С может иметь любое положение на окружности.
С

![]()
![]()
![]()
А О В
Рисунок 9.
В частном случае, когда частица с массой![]() до столкновения покоится в JI-системе, имеем:
до столкновения покоится в JI-системе, имеем:
![]() ,
,![]() , (2.4 13)
, (2.4 13)
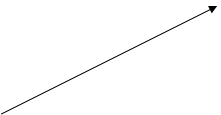
т.е. на диаграмме т. В лежит на окружности; ОВ = ОС - радиус, вектор![]() совпадает с импульсом
совпадает с импульсом![]() первой частицы до удара. При этом точка А может находиться внутри (если
первой частицы до удара. При этом точка А может находиться внутри (если ![]() ) или вне (если
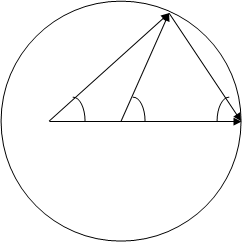
) или вне (если ![]() ) окружности (рисунок 10). Несложно показать, что углы
) окружности (рисунок 10). Несложно показать, что углы ![]() и
и ![]() отклонения частиц после столкновения по отношению к
отклонения частиц после столкновения по отношению к ![]() (к направлению удара) могут быть выражены через угол
(к направлению удара) могут быть выражены через угол ![]() поворота первой частицы в Ц-системе:
поворота первой частицы в Ц-системе:
![]() ,
,![]() , (2.4 14)
, (2.4 14)


 С С
С С
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
А О ![]() В А О
В А О ![]() В
В
Рисунок 10.
Модули скоростей частиц после удара в Л-системе также могут быть выражены через угол ![]() и модуль относительной скорости
и модуль относительной скорости![]() до удара:
до удара:
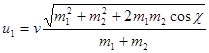 ,
,
![]() . (2.4 15)
. (2.4 15)
Отметим, что сумма![]() определяет угол разлета частиц после столкновения. При
определяет угол разлета частиц после столкновения. При ![]() эта сумма больше
эта сумма больше![]() , при
, при![]() - меньше
- меньше ![]() , угол разлета частиц равной массы прямой.
, угол разлета частиц равной массы прямой.
Заключение
В ряде случаев векторный способ имеет преимущество перед координатным, не только упрощая решение конкретной задачи, но и превращая иногда сложные на первый взгляд задачи в подстановочные, решаемые практически устно.
В работе рассмотрены возможности использования одного из не-стандартных методов решения задач механики в курсе физики средней школы. Основные результаты можно сформулировать следующим обра-зом:
1. Показана роль решения задач при обучении физике, приведены алгоритмы решения задач координатным способом.
2. Сформулированы теоретические основы векторных способов решения избранных задач кинематики и динамики.