Курсовая работа: Викладення теми Трикутники по програмі курсу геометрії в 7 класі середньої школи

Рис.2.1 До теореми 2.1 (ознака рівності трикутників по двох сторонах і куту між ними) [8]

Доведення.

Нехай у трикутників й - дві сторони та кут між ними рівні: (див. рис.2.1). Доведемо, що трикутники рівні.

Нехай - трикутник, дорівнює трикутнику , з вершиною на промені й вершиною в тій же напівплощині відносно прямій , де лежить вершина (рисунок 2.2, а).

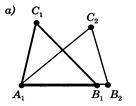
Рис.2.2, а) До доведення 1 признаку рівності трикутників [8]

Тому що , то вершина збігається з вершиною (див. рис.2.2, б).

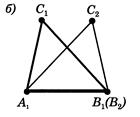
Рис.2.2, б) До доведення 1 признаку рівності трикутників [8]

Тому що то промінь збігається із променем

(див. рис.2.2, в).

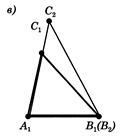
Рис. .2.2, в) До доведення 1 признаку рівності трикутників [8]

Тому що =, то вершина збігається з вершиною (рис.2.2, г).

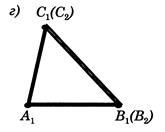
Рис.2.2, г) До доведення 1 признаку рівності трикутників [8]

Отже, трикутник збігається із трикутником , виходить, дорівнює трикутнику .

Теорема доведена.

Теорема 2.2 (Друга ознака рівності трикутників по стороні й прилеглим до неї кутам).

Якщо сторона й прилеглі до неї кути одного трикутника рівні відповідно стороні й прилеглим до неї кутам іншого трикутника, то такі трикутники рівні.

Доведення.

Нехай і - два трикутники, у яких

(рисунок 2.3).

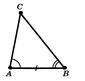
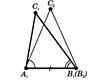
Рис.2.3 До доведення 2ї ознаки рівності трикутників [8]

Доведемо, що трикутники рівні. Ð

Нехай - трикутник, дорівнює трикутнику з вершиною на промені й вершиною в тій же напівплощині відносно прямій , де лежить вершина .

Тому що , то вершина збігається з вершиною . Тому що й , то промінь збігається із променем , а промінь збігається із променем . Звідси витікає, що вершина збігається з вершиною .

Отже, трикутник збігається із трикутником , а виходить, дорівнює трикутнику .