Курсовая работа: Викладення теми Трикутники по програмі курсу геометрії в 7 класі середньої школи

Теорема 2.3 (Третя ознака рівності трикутників по трьох сторонах).

Якщо три сторони одного трикутника рівні відповідно трьом сторонам іншого трикутника, то такі трикутники рівні.

Доведення.

Нехай і два трикутники, у яких . Потрібно довести, що трикутники рівні.

Допустимо, трикутники не рівні. Тоді в них . Інакше вони були б рівні по першій ознаці.

Нехай - трикутник, дорівнює трикутнику , у якого вершина лежить в одній напівплощині з вершиною відносно прямій (рисунок 2.4).

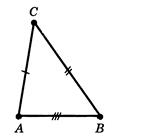
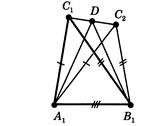
Рис.2.4 До доведення 3 признаку рівності трикутників [8]

Нехай середина відрізка й - рівнобедрені із загальною основою . Тому їхні медіани й перпендикуляри прямої . Прямі й не збігаються, тому що точки не лежать на одній прямій. Але через точку прямої можна провести тільки одну перпендикулярну їй пряму. Ми прийшли до протиріччя

Теорема доведена.

Задача 2.1 Відрізки й перетинаються в точці , що є серединою кожного з них. Чому дорівнює відрізок , якщо відрізок м?

Розв’язок. Трикутники й рівні по першій ознаці рівності трикутників (рисунок 2.5).

Рис.2.5 До задачі 2.1 [8]

У них кути й рівні як вертикальні, а й тому, що точка є серединою відрізків і . З рівності трикутників і треба рівність їхніх сторін і . А тому що за умовою задачі м, те й м.

Задача 2.2 У трикутників і . Доведіть, що .

Розв’язок. Нехай і дані трикутники (рисунок 2.6).

Рис.2.6 До задачі 2.2 [8]

Побудуємо трикутник , який дорівнює трикутнику , і трикутник , який дорівнює трикутнику .

Трикутники й рівні по третій ознаці. У них за умовою задачі; тому що ; , тому що . З рівності трикутників і треба рівність кутів . Тому що за умовою ,, а , по доведеному, то трикутники й рівні по першій ознаці.

3. Рівнобедрений трикутник, його властивості та ознаки

Трикутник називається рівнобедреним, якщо в нього дві сторони рівні. Ці рівні сторони називаються бічними сторонами, а третя сторона називається основою трикутника.

На рисунку 3.1 зображений рівнобедрений трикутник . У нього бічні сторони й , а основа.

Рис.3.1 До визначення рівнобедреного трикутника [8]

Теорема 3.1 (властивість кутів рівнобедренного трикутника)

В рівнобедренному трикутнику кути при основі рівні.

Доведення.

Нехай - рівнобедрений трикутник з основою (див. рис.3.2). Доведемо, що в нього .