Курсовая работа: Викладення теми Трикутники по програмі курсу геометрії в 7 класі середньої школи

Задача 6.1. Доведіть, що в прямокутному трикутнику з кутом катет, протилежний цьому куту, дорівнює половині гіпотенузи.

Рішення. Нехай - прямокутний трикутник із прямим кутом і кутом , рівним (рисунок 6.3).

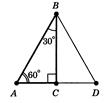
Рис.6.3. До задачі 6.3 [8]

Побудуємо трикутник , який дорівнює трикутнику , як показано на Рис.6.3.

У трикутника всі кути рівні , тому він рівносторонній. Тому що , а , то . Що й було потрібно довести.

7. Зовнішній кут трикутника та його властивості

Зовнішнім кутом трикутника при даній вершині називається кут, суміжний з кутом трикутника при цій вершині (рисунок 7.1).

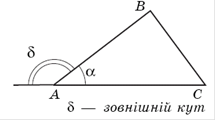
Рис.7.1. До визначення зовнішнього кута трикутника [5]

Щоб не плутати кут трикутника при даній вершині із зовнішнім кутом при цій же вершині, його іноді називають внутрішнім кутом.

Теорема 7.1. Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів не суміжних з ним.

Доведення.

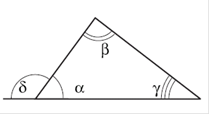
Нехай - даний трикутник (рисунок 7.2).

Рис.7.2. До теореми 7.1 [5]

По теоремі про суму кутів трикутника

.

Звідси витікає, що

.

У правій частині цієї рівності стоїть градусна міра зовнішнього кута d трикутника.

Теорема доведена.

З теореми 7.1 витікає, що зовнішній кут трикутника більше будь-якого внутрішнього кута, не суміжного з ним. Задача 7.1. У трикутнику проведена висота . Яка із трьох точок лежить між двома точками, якщо кути й трикутника гострі? Рішення. Точка не може лежати між точками й (рисунок 7.3),

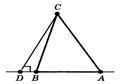
Рис. .7.3. До задачі 7.1 [8]

то гострий кут як зовнішній кут трикутника був би більше прямого кута . Точно так само доводиться, що й точка не може лежати між точками й . Виходить, точка лежить між точками й .

8. Нерівність трикутника

Якщо точки й різні, то відстанню між ними називається довжина відрізку . Якщо точки й збігаються, то відстань між ними приймається рівною нулю.

Теорема 8.1 (нерівність трикутника).

Які б не були три точки, відстань між будь-якими двома із цих точок не більше суми відстаней від них до третьої точки.