Курсовая работа: Використання інтегралів в економіці

Звідси одержуємо важливу формулу інтегрування частинами визначеного інтеграла.

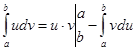(8)

Приклад 2. Обчислити інтеграл xcosxdx.

Розв'язування. Нехай u = x, dv = cosxdx , тоді знаходимо du = dx, (взята первісна без сталої С). Застосовуючи до заданого інтеграла формулу (8), одержимо

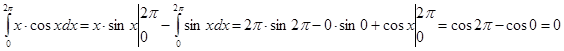
Теорема 4. Нехай задано інтеграл , де f (х) неперервна на відрізку [а,b]. Зробимо підстановку х = (t), аtß, де (t) неперервно диференційована функція на відрізку [,ß].

Якщо: при зміні t від до ß змінна х змінюється від а до b, тобто (а)= а, (ß) = b; складна функція f[(t)] визначена і неперервна на відрізку [,ß], тоді має місце рівність

(9)

Доведення. Нехай F(x) деяка первісна для функції f (х), тобто F'(X) = f (х). Розглянемо складну функцію F [(t)]. Застосовуючи правило диференціювання складної функції, одержимо

Це означає, що функція F[(t)] є первісною для функції

Звідси, за формулою Ньютона-Лейбніца і рівностей () = a та (ß) = b, одержуємо

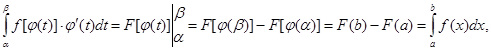
що й треба було довести.

Приклад 3. Обчислити

.

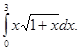Розв’язування. Нехай t = , тоді t2 = 1 + хх = t2 - 1, dx= 2tdt. Знайдемо межі інтегрування, використовуючи рівність

Отже,

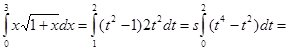
Для деяких неперервних надінтегральних функцій f (х) первісну не можна виразити елементарними функціями. У цих випадках обчислення визначного інтеграла за формулою Ньютона-Лейбніца неможливе [4].

Крім того, у практичній діяльності часто досить знати лише наближене значення визначеного інтеграла і знаходити це наближене значення такими методами, які дозволяють використовувати сучасну обчислювальну техніку.

Тому математики багатьох країн розробляють ефективні методи наближеного обчислення визначеного інтеграла.

Найбільш часто використовують три методи — метод прямокутників, метод трапецій та метод парабол (метод Сімпсона).

Якщо відрізок інтегрування [а,b] поділити на n рівних частин довжиною

і позначити через середню точку відрізку визначений інтеграл можна обчислити за формулою