Курсовая работа: Використання інтегралів в економіці

яку називають формулою прямокутників. Чим більше буде n, тим менше буде крок

і права частина (10) буде давати більш точне значення інтеграла.

Якщо поділити відрізок інтегрування точками ділення

а = х0 < x1 < х2 < ... < хk < ... < хn-1 < хk = b

на n рівних частин довжиною

i позначити значення функції в точках ділення f (хk), тоді визначений інтеграл можна обчислити за формулою

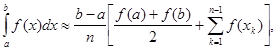(11)

яку називають формулою трапецій. Легко бачити, що при зростанні n крок

зменшується, тому значення інтеграла буде більш точним.

Якщо відрізок інтегрування [а,b] поділити на парну кількість рівних частин (тобто n = 2m) i позначити уk = f (xk), де xk = а + х·k — точки ділення, k = 0, 1, ..., 2m, тоді визначений інтеграл можна обчислити за формулою

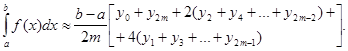(12)

яку називають формулою Сімпсона. Ця формула дає більш точне значення визначеного інтеграла тому, що для її доведення використовується метод парабол, за яким на кожному відрізку [xk-1, xk] три значення функції f (х) входять до інтегральної суми.

Розділ 2. Практичне застосування визначеного інтегралу в економіці

Останнім часом з'явилася велика кількість шкіл і класів, учні яких вибирають економічні спеціальності як своя подальшу діяльність. Як правило, учителя, що працюють у таких класах, дають учням більш глибокі знання по звичайних темах шкільного курсу математики, найчастіше орієнтуючись на програми для шкіл і класів з поглибленим вивчанням математики. Але при такій організації навчання практично не розглядаються економічні додатки тієї або іншої теми, мало часу приділяється застосуванню математичного моделювання до рішення економічних завдань. Не є виключенням і тема, присвячена застосуванню певного інтеграла в інших областях знань.

Традиційно практичний додаток інтеграла ілюструється обчисленням площ різних фігур, знаходженням обсягів геометричних тіл і деяких додатків у фізиці й техніці. Однак роль інтеграла в моделюванні економічних процесів не розглядається. Найчастіше про економічні додатки інтеграла не йде мови й у класах економічного напрямку. Разом з тим, інтегральне вирахування має багатий математичний апарат для моделювання й дослідження процесів, що відбуваються в економіці [4].

Зупинимося на декількох прикладах використання інтегрального вирахування в економіці. Почнемо із широко використовуваного в ринковій економіці поняття споживчого надлишку. Для цього введемо кілька економічних понять і позначень.

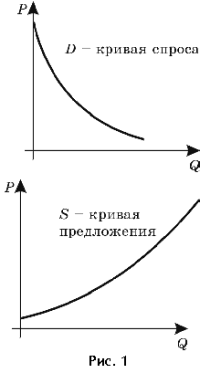
Попит на даний товар - сформована на певний момент часу залежність між ціною товару й обсягом його покупки. Попит на окремий товар графічно зображується у вигляді кривої з негативним нахилом, що відбиває взаємозв'язок між ціною P одиниці цього товару й кількістю товару Q, що споживачі готові купити при кожній заданій ціні. Негативний нахил кривої попиту має очевидне пояснення: чим дорожче товар, тим менше кількість товару, що покупці готові купити, і навпаки.

Аналогічно визначається й інше ключове поняття економічної теорії - пропозиція товару: сформована на певний момент часу залежність між ціною товару й кількістю товару, пропонованого до продажу. Пропозиція окремого товару зображується графічно у вигляді кривої з позитивним нахилом, що відбиває взаємозв'язок між ціною одиниці цього товару P і кількістю товару Q, що споживачі готові продати при кожній ціні.

Відзначимо, що економісти порахували зручним зображувати аргумент (ціну) по осі ординат, а залежна змінну (кількість товару) по осі абсцис. Тому графіки функцій попиту та пропозиції виглядають у такий спосіб (малюнок 1).

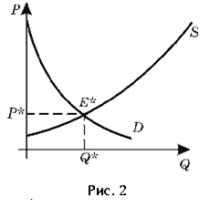
І, нарешті, уведемо ще одне поняття, що грає більшу роль у моделюванні економічних процесів - ринкова рівновага. Стан рівноваги характеризують такі ціна й кількість, при яких обсяг попиту збігається з величиною пропозиції, а графічно ринкова рівновага зображується точкою перетинання кривих попиту та пропозиції (малюнок 2), E*(p*; q*) - точка рівноваги.

Надалі для зручності аналізу ми будемо розглядати не залежність Q = f(P), а зворотні функції попиту та пропозиції, що характеризують залежність P = f(Q), тоді аргумент і значення функції графічно будуть зображуватися звичним для нас образом.

Перейдемо тепер до розгляду додатків інтегрального аналізу для визначення споживчого надлишку. Для цього зобразимо на графіку зворотну функцію попиту P = f(Q). Допустимо, що ринкова рівновага встановилася в точці E*(q*; p*) (крива пропозиції на графіку відсутній для зручності подальшого аналізу, малюнок 3).

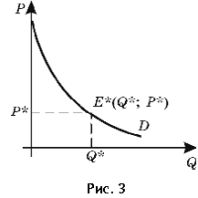
Якщо покупець здобуває товар у кількості Q* за рівноважною ціною P*, то очевидно, що загальні витрати на покупку такого товару складуть P*Q*, що дорівнює площі заштрихованої фігури A (малюнок 4).