Курсовая работа: Вивчення систем, еквівалентних системам з відомим типом крапок спокою
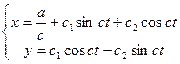 , якщо з
, якщо з![]() 0;
0;
x=0, y=at+c![]() , якщо з=0, де постійні з, з
, якщо з=0, де постійні з, з![]() , зі
, зі![]() зв'язані співвідношенням з
зв'язані співвідношенням з![]() (b+c
(b+c![]() +c
+c![]() ) =a
) =a![]() , має два центри в крапках
, має два центри в крапках![]()
![]() і
і ![]() .
. ![]() Рішення:
Рішення:
Підставимо загальне рішення
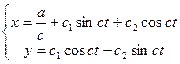
у нашу систему (1) одержимо
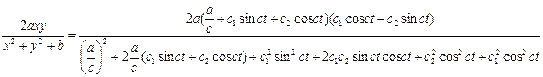
![]()
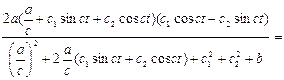
=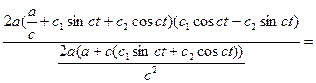
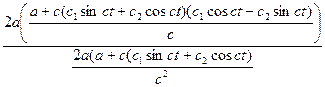 =c (c
=c (c![]() cosct-c
cosct-c![]() sinct) =
sinct) =![]()
a-![]()
![]()
Для стислості розпишемо знаменник і перетворимо
x![]() +y
+y![]()
+b=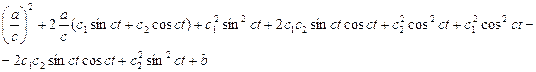
![]()
![]()
![]()
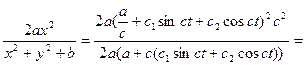
![]()
=a+c (c![]() sinct+c
sinct+c![]() cosct)
cosct)
a-![]()
![]()
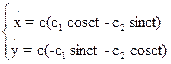
Одержуємо, що x і y є загальним рішенням системи.
3. Знаходження першого інтеграла диференціальної системи й умови його існування
Розглянемо систему ![]() = f (t, x), x= (x
= f (t, x), x= (x![]() ,…,x
,…,x![]() ), (t,x)
), (t,x) ![]() (1) с безперервної в області D функцією f. Функція U (t, x), задана в деякої під області G області D, називається першим інтегралом системи (1) в області G, якщо для будь-якого рішення x (t), t
(1) с безперервної в області D функцією f. Функція U (t, x), задана в деякої під області G області D, називається першим інтегралом системи (1) в області G, якщо для будь-якого рішення x (t), t![]() , системи (1), графік якого розташований в G функція U (t, x (t)), t
, системи (1), графік якого розташований в G функція U (t, x (t)), t![]() , постійна, тобто U (t, x (t)) залежить тільки від вибору рішення x (t) і не залежить від t.
, постійна, тобто U (t, x (t)) залежить тільки від вибору рішення x (t) і не залежить від t.
Нехай V (t, x), V: G![]() R , є деяка функція. Похідній від функції V у силу системи (1) назвемо функцію V
R , є деяка функція. Похідній від функції V у силу системи (1) назвемо функцію V![]() V
V![]() R, обумовлену рівністю
R, обумовлену рівністю
V![]() (t, x (t))
(t, x (t)) ![]() t
t![]() .
.
Лема 1.
Для будь-якого рішення x (t), t![]() , системи (1), графік якого розташований в G, має місце тотожність
, системи (1), графік якого розташований в G, має місце тотожність
V![]()
![]() t
t![]() .
.
Без доказу.