Курсова робота

"Вивчення систем, еквівалентних системам з відомим типом крапок спокою"

Реферат

Курсова робота складається з _____ сторінок, 3-х джерел.

Ключові слова: вложима система, з відомим типом крапок спокою, перший інтеграл диференціальної системи, функція, клас систем еквівалентних системі з відомим типом крапок спокою.

Метою курсової роботи є дослідження системи з відомим типом крапок спокою, знаходження першого інтеграла системи, застосування теореми про еквівалентність диференціальних систем.

Зміст

Введення

1. Визначення вложимої системи. Умови вложимості

2. Загальне рішення системи

3. Знаходження першого інтеграла диференціальної системи й умови його існування

4. Функція, що відбиває

5. Застосування теореми про еквівалентність диференціальних систем

Висновок

Список джерел

Введення

У курсовій роботі розглядається вложима система з відомим типом крапок спокою. Як відомо система є вложимою, якщо будь-який компонент цієї системи вложима, тобто система вложима тоді й тільки тоді, коли множина її рішень є підмножиною множини рішень деякої лінійної стаціонарної системи.

В 1-2 м пунктах розглядається вложима система, з відомим типом крапок спокою. Далі перевіряємо чи є x і y загальним рішенням нашої системи рівнянь.

В 3-м ми знаходимо перший інтеграл системи й перевіряємо виконання тотожності.

В 4-м пункті досліджуємо функції, що відбивають

В 5-м пункті застосовуємо теорему про еквівалентність диференціальних систем

1. Визначення вложимої системи. Умови вложимості

Розглянемо диференціальну систему

D. (1)

Будемо називати i-ю компоненту x системи (1) вложимої, якщо для будь-якого рішення x (t) = (x (t),…,x (t)),t, цієї системи функція x t, є многочленом. У такий спосіб i-я компонента системи (1) вложима тоді й тільки тоді, коли для кожного рішення x (t) цієї системи існує лінійне стаціонарне рівняння виду

, (2)

для якого є рішенням. Загалом кажучи, порядок і коефіцієнти рівняння (2) залежать від вибору рішення . В окремому випадку, коли компонента будь-якого рішення системи (1) є одночасно й рішенням деякого, загального для всіх рішень рівняння (2), компоненту системи (1) будемо називати сильно вложимої у рівняння (2).

2. Загальне рішення системи

Розглянемо вложиму систему

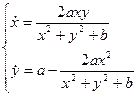(1)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--