Поряд з диференціальною системою 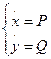(1) розглянемо обурену систему 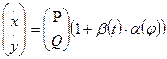(2), де - будь-яка безперервна непарна функція. Відомо по [3], що диференціальна система (3) еквівалентна обуреній системі (4), де безперервна скалярна непарна функція задовольняючому рівнянню

Тому що вище вже показано, що функція де {є перший інтеграл} задовольняє цьому рівнянню, те справедлива наступна теорема.

Теорема 1.

Система 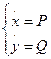(1) еквівалентна системі 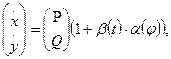(2) у змісті збігу функції, що відбиває.

Тому що система 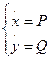(1) має дві особливі крапки, у кожній з яких перебуває центр, те й система 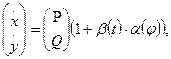(2) має центри в цих крапках.

Висновок

У даній курсовій роботі розглянута вложима система з відомим типом крапок спокою, перевірене задоволення загального рішення нашій системі, знайдені перший інтеграл і перевірений виконання тотожності, потім за допомогою теореми 1 доведена еквівалентність диференціальних систем. Сформульовано визначення вложимої системи, першого інтеграла, що відбиває функції й загальні властивості функції, що відбиває. Сформульована теорема за допомогою якої ми довели еквівалентність нашої системи з диференціальною системою.

Список джерел

1. Мироненко В.І. Лінійна залежність функцій уздовж рішень диференціальних рівнянь. - К., 2001.

2. Мироненко В.І. Функція, що відбиває, і періодичні рішення диференціальних рівнянь. - К., 2004.

3. Мироненко В.І. Збурювання диференціальних систем, що не змінюють тимчасових симетрій. - К., 2004 р.