Після вище зроблених перетворень одержуємо, що функція - це перший інтеграл системи (1), 2) Покладемо , тобто , де , Q

3) Перевіримо виконання тотожності:

(3), де

Перетворимо (3).

[у нашім випадку ] =

=

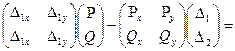
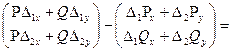
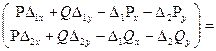
[з огляду на всі зроблені позначення] =

=

=

=

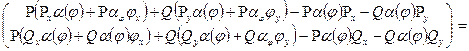
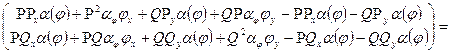
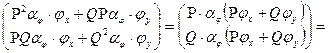
[через те, що котре у свою чергу як ми вже показали їсти тотожний нуль]

Таким чином, тотожність (3) щире.

4. Функція, що відбиває

Визначення. Розглянемо систему

(5)

вважає, що права частина якої безперервна й має безперервні частки похідні по . Загальне рішення у формі Коші позначений через ). Через позначимо інтервал існування рішення . Нехай

функцією, що відбиває, системи (5) назвемо функцію , обумовлену формулою

Для функції, що відбиває, справедливі властивості:для будь-якого рішення системи (5) вірна тотожність

для функції, що відбиває, F будь-якої системи виконані тотожності

3) функція буде функцією, що відбиває, системи (5) тоді й тільки тоді, коли вона задовольняє системі рівнянь у частинних похідних

і початковій умові

5. Застосування теореми про еквівалентність диференціальних систем