Курсовая работа: Вивчення систем з постійною парною частиною

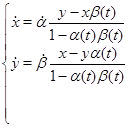(13)

Системи виду (13) будуть мати сімейства рішень із постійною парною частиною. У цьому легко переконається, проробивши обчислення, аналогічні попереднім прикладам.

5. Прості й найпростіші системи

Лема 9 Для всякої безупинно диференцюємої функції

для якої виконані тотожності (4), мають місце співвідношення

Теорема 10 Для всякої двічі безупинно диференцюємої функції певної в симетричній області , що містить гіперплощина для якої виконані тотожності (4), існує диференціальна система c безупинно диференцюємої правою частиною, що відбиває функція якої збігається с.

Теорема 11 Для всякої двічі безупинно диференцюємої функції

певної в області утримуюча гіперплощина , для якої виконані тотожності (4), при всіх і досить малих існує диференціальна система

функція, що відбиває, якої збігається з а загальний інтеграл задається формулою

Наслідок 12 Двічі безупинно диференцюєма функція

є функцією, що відбиває, хоча б однієї диференціальної системи тоді й тільки тоді, коли для неї виконані (4)тотожності .

Системи, існування яких гарантується теоремами 10 й 11, називаються відповідно простій і найпростішої.

Теорема 13 Нехай

найпростіша система, тоді

де – функція, що відбиває, (1)системи .

Доказ. Якщо система найпростіша,

Теорема 14 Нехай