Курсовая работа: Жизнь и деятельность семьи Бернулли
Бернулли принадлежит одна из первых формулировок закона сохранения энергии (живой силы, как тогда говорили), а также (одновременно с Эйлером) первая формулировка закона сохранения момента количества движения (1746). Он много лет изучал и математически моделировал упругие колебания, ввёл понятие гармонического колебания, дал принцип суперпозиции колебаний.
В математике опубликовал ряд исследований по теории вероятностей, теории рядов и дифференциальным уравнениям. Он первый применил математический анализ к задачам теории вероятностей (1768), до этого использовались только комбинаторный подход. Бернулли продвинул также математическую статистику, рассмотрев с применением вероятностных методов ряд практически важных задач.
Даниил являлся Академиком и почетным иностранным членом Петербургской академии наук(1733), членом Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750). Лауреат многочисленных премий и призов в конкурсах.
Якоб II Бернулли
Якоб получил юридическое образование, но затем переключился на физику и математику. После неудачной попытки занять кафедру физики в Базеле, освободившуюся после смерти Даниила Бернулли (1782), Якоб уехал в Италию и поступил на дипломатическую службу. В 1786 году он переселился в Россию. Женился на внучке Эйлера. Служил в Академии наук и Кадетском корпусе. Погиб в возрасте 30 лет в результате несчастного случая при купании в Неве.
Якоб Бернулли успел опубликовать незаурядные работы по различным вопросам механики, теории упругости, гидростатики и баллистики: вращательному движению тела, укрепленного на растяжимой нити, течению воды в трубах, гидравлическим машинам. Вывел дифференциальное уравнение колебания пластин.
Математические объекты, названные в честь членов семьи
Дифференциальное уравнение вида:
![]() с, n≠1, 0.
с, n≠1, 0.
называется дифференциальным уравнением Бернулли (в честь Якоба).
Метод решения:
1. Делим левую и правую части на yn
![]()
2. Выполняем замену
![]()
![]()
3. Решаем дифференциальное уравнение
![]()
Оно может быть решено с использованием интегрирующего множителя
![]()
Пример:
![]()
Делим на y 2
![]()
Замена переменных

Умножаем на M (x) ,
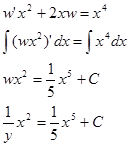
Результат
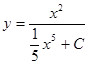
Закон Бернулли
Закон Бернулли (в честь Даниила Бернулли) является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости: