Лабораторная работа: Кривошипно-ползунный механизм, его структура, схема, анализ

Этот метод применяется для анализа движущихся механизмов при известных массах и моментах инерции звеньев.

Для этого разбиваем механизм на структурные группы Ассура и начинаем вычерчивать с последней группы звеньев (группы, связанной с выходным звеном).

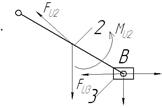
Рисунок 6 – Структурная группа Ассура 1

Разорванную связь 1-2 заменяем реакцией R₁₂ , раскладывая ее на составляющие и , а нормаль XX реакцией R₀₃ . Составляем уравнение равновесия:

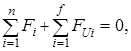(31)

(32)

Уравнение равновесия (32) содержит три неизвестных , и , следовательно, его статическая неопределимость равна двум.

С целью раскрытия статической неопределимости найдем модуль.

Звено АВ:

(33)

В результате проведенных вычислений уравнение (32) содержит две неизвестных и , следовательно статическая неопределимость раскрыта полностью. Уравнение равновесия примет следующий вид:

(34)

Определение оставшихся неизвестных выполним с помощью плана сил. Для этого необходимо выбрать масштабный коэффициент плана сил:

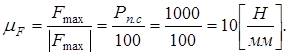(35)

Переведем в масштабный коэффициент оставшиеся силы:

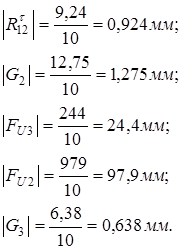(36)

По полученным величинам строим план сил в масштабном коэффициенте (рисунок 7).

По построенному плану сил определяем неизвестные , и :

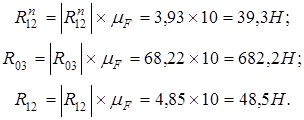(37)

Рассмотрим первичный механизм.

Направляем уравновешивающую силу перпендикулярно оси кривошипа, в противоположную сторону вращения оси кривошипа. Вектор выходит из подвижной точки кривошипа.

Составляем уравнение равновесия:

(38)

Составляем уравнение моментов сил относительно точки O:

(39)

Из уравнения (4.23) определяем :