Лабораторная работа: Парный регрессионный анализ

Следовательно, r_xy = 0,103152553. Значит можно сделать вывод, что между х и у, то есть между постоянными расходами и объемом выпускаемой продукции не наблюдается никакой связи.

Рассчитаем коэффициент детерминации:

D = r² _xy * 100

D = 1,064044912%

Следовательно, величина постоянных расходов только на 1,064044912% объясняется величиной объема выпускаемой продукции.

2. Рассчитаем дисперсионное отношение Фишера:

, где n – число регионов

Следовательно, n = 36

F _расч = 0,150568403

Найдем F_{табличное} : k₁ = m, m = 1(т.к. на y влияет только один фактор х),

k₂ = n- m-1. Значит k₁ = 1, k₂ = 36-1-1= 34. Находим табличное значение F на пересечении k₁ и k_2. Получаем, что F_{табличное} = 2,145.

Так как F_{расчетное} < F_{табличное} значит уравнение статистически не значимо.

3. Рассчитаем стандартные ошибки коэффициентов регрессии:

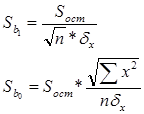
где

Для этого надо еще добавить в таблицу значения y - , (y - )² , и рассчитать общую сумму по 36 регионам и их среднее значение.

При вычислении S_ост было получено, что

S_ост = 382,9325409.

Следовательно,

S_b1 = 27,7984546,

S_b0 = 918,3564058

4. Рассчитаем доверительные границы коэффициентов регрессии:

, где

t_табл находится по таблице t-критерия Стьюдента при уровне значимости 0,05 и числе степенной свободы равной 34.

Значит t_табл =2,145.

= 1969,87449

= 59,62768512

Следовательно, можно рассчитать доверительные границы коэффициентов регрессии: