Научная работа: Доказательство Великой теоремы Ферма с помощью метода бесконечных (неопределенных) спусков

где к – любое действительное число, аi - произвольный нумератор решений множества решений

I состоящее из решений совокупности связанных решений ( a_{i ,} b_{i ,} c_i ) определяемых через любое существующее решение ( a ’, b ’, c ’) .

Таким образом, i -тое решение уравнения a ² + b ² = c ² позволяет нам найти определить I -тое коммутативное множество решений уравнения.

Принципиальная невозможность решения уравнения a ² + b ² = c ² позволяет нам утверждать невозможности получения всего множества решений уравнения.

Верификация метода бесконечных (неопределенных) спусков:

Стороны уравнения a ² + b ² = c ² в силу закона ассоциативности могут быть умножены на любое рациональное число К выраженное через действительное число к в виде К = к ² : мы можем сделать преобразование и в целых числах a ', b ’, c ’ представить уравнение a ² + b ² = c ² выражением в виде:

К · ( a ’ ² + b ’ ² ) = К · c ’ ²

в силу закона дистрибутивности (или распределительности) можно сделать следующее преобразование и получить выражение в виде:

K · a ’² + K · b ’² = K · c ’²

где К – любое рациональное число и К = к ² где к – любое действительное числоследующее преобразование приводит уравнение

aⁿ + bⁿ = cⁿ к виду:

k² a² + k² b² = k² c²

(ka)² + (kb)² = (kc)²

где К – любое рациональное число K ∈ { Q } ,где Q – поле рациональных чисел, образованное из действительного числа k по формуле К = k ^{2 ,} где число k ∈ { R } ,где R – поле действительных чисел

Действительное число к множества действительных чисел – позволяет работать во всем действительном числовом поле решений, представленных в виде ( k_i a ’, k_i b ’, k_i c ’) даже при единственном возможном решении гдеa ', b ’, c ’ – целые числа

Множество всех действительных чисел составляют натуральные, целые, рациональные и иррациональные числа

N ⊂ Z ⊂ Q ⊂ R , J ⊂ R решения { k_i a ’, k_i b ’, k_i c ’ } ⊂ R .

Это значит, что если не существует решения a ² + b ² = c ² ( a ', b ’, c ’) не существует и ни одного решения ( k_i a ’, k_i b ’, k_i c ’) во всем множестве целых чисел

(a , b , c ) ⊂ Z

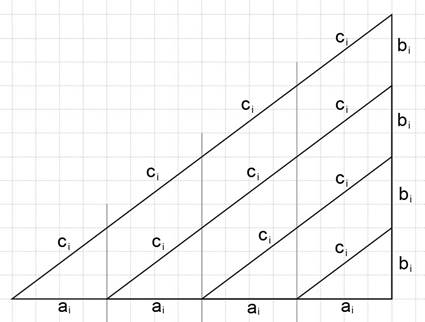
Верификация метода бесконечных (неопределенных) спусков в геометрическом виде представлена[2] на рис. 1 :

рис. 1

Возможность получения бесконечного множества I пропорциональных решений при известном i -том решении прямоугольного треугольника и поможет нам в разрешении поставленной задачи.

Теперь, собственно, перейдем к доказательству Великой теоремы (утверждения) Ферма:

уравнение a ⁿ + b ⁿ = c ⁿ при натуральномn ⊂ N , n > 2 ,не имеет решения в ненулевых целых числах а’ , b ’, c ’ , { a ’, b ’, c ’} ⊂ Z ,

Рассмотрим уравнение:

a ⁿ + b ⁿ = c ⁿ

Уравнение aⁿ + bⁿ = cⁿ можно представить в виде

( a^{n -2} ) · a ² +( b^{n -2} ) · b ² = ( c^{n -2} ) · c ²

Предположим , что уравнение aⁿ + bⁿ = cⁿ имеет решение в целых числах а’ , b ’, c ’