Научная работа: Доказательство Великой теоремы Ферма с помощью метода бесконечных (неопределенных) спусков

И наоборот, уравнение 1² + 1² = c ² не будет иметь решения в рациональных числах, если отсутствует такое рациональное число, которое может быть образовано от рационального числа к с помощью умножения на само себя и будет равно двум (К = 2 )

К = к ² , а не наоборот, когда к = √ К

Если число к не определено на числовой прямой рациональных чисел, то его умножение в рациональном выражении возможно только с определенными условностями (например – округлением).

Это рассуждение, основанное на методе П.Ферма - бесконечных (неопределенных) спусков является источником объяснения того, что

1² + 1² = c ²

не будет иметь решений в рациональных числах, если нет такого рационального числа, которое умноженное на само себя будет равно двум.

И будет иметь решение в действительных числах, т.к. величинак которое образует число к ² = 2 имеет существующую зависимость от существующей величины, а значит существует.

Величина 1² + 1² - существует, существует действие умножения 1 · 1 ^, значит существует и величина k · k .

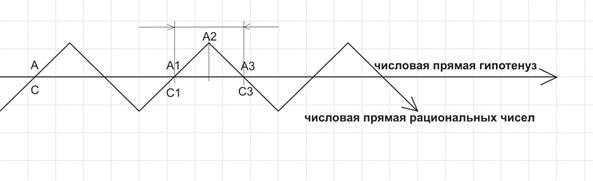
Т.е. про число к , которое образует число к ² = 2 мы можем говорить лишь о том, что эта величина к существует, это действительное число, но мы да данном этапе не имеем особой меры гипотенуз (числовой оси гипотенуз), и поэтому не можем представить ее в поле мерных величин - особых рациональных числахмерного числового пространства.

____________________________

© А.В. Тарасов

07. 01. 2008 г.

[1] Из разных источников

[2] Возможно, эта формула может служить источником объяснения иррациональности корня из 2, то есть невозможности решений уравнений для к = с в рациональных числах.