Научная работа: Исследование процесса вытяжки заготовки "стакан"

Рис. 36. Распределение интенсивности деформации по сечению заготовки на 70 этапе нагружения.

Рис. 37. Распределение интенсивности деформации по сечению заготовки на 100 этапе нагружения.

На рис. 38- представлены графики изменения компонентов напряжения и компонентов деформации.

Рис. 38. Изменение компонентов напряжения по ходу нагружения для точки 1 при (вариант 2).

Рис. 39. Изменение компонентов деформации по ходу нагружения для точки 1 при (вариант 2).

Радиальная и осевая компоненты по ходу нагружения в данном случае практически не отклоняются от нулевого значения, а окружная компонента находится в зоне сжатия. Осевая и радиальная компоненты деформации находятся в зоне растяжения, а окружная в зоне сжатия. Резкий скачек компонент напряжения и радиальной и осевой компонент деформации на 94 шаге обуславливается втягиванием концевой части заготовки в зазор между матрицей и пуансоном.

Рис. 40. Изменение компонентов напряжения по ходу нагружения для точки 2 при (вариант 2).

Рис. 41. Изменение компонентов деформации по ходу нагружения для точки 2 при (вариант 2).

Установлено, что осевая и радиальная компоненты напряжения в зоне растяжения до 50 шага возрастают, а затем падают до 0; окружная компонента на 18 шаге переходит из зоны растяжения в зону сжатия. Радиальная и осевая компоненты деформации находятся в зоне растяжения и зоне сжатия соответственно.

Рис. 42. Изменение компонентов напряжения по ходу нагружения для точки 3 при (вариант 2).

Рис. 43. Изменение компонентов деформации по ходу нагружения для точки 3 при (вариант 2).

Укажем, что все компоненты напряжений являются растягивающими. Радиальная и осевая компоненты деформации находятся в зоне сжатия и зоне растяжения соответственно.

На рис. 44 представлен график силы вытяжки.

Рис. 44. Сила вытяжки (вариант 2); 1 – практическая зависимость; 2 – теоретическая зависимость.

По силе можно проследить, что оно начинает резко возрастать, когда заготовка входит в матрицу. Усилие продолжает расти из-за того, что донная часть детали начинает утоняться из-за сил трения, возникающих на поверхности матрицы, т.к. большая часть металла уже вошла в зазор между пуансоном и матрицей. Спад силы приходится на момент, когда начинается разгрузка на боковых стенках заготовки. Рассмотрев графики на рис. 40 можно сделать вывод о том, что характер кривых в зависимостях, полученных теоретически и при расчете математической модели, практически идентичны.

Для задачи с зазором равным толщине заготовки:

коэффициент вытяжки составляет md = ;

коэффициент утонения стенки: mS =;

действительный коэффициент утонения стенки с учетом утолщения краевой части заготовки ;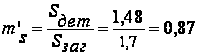

достижимые значения коэффициентов md и mS составляют соответственно 0,44 и 1,0;

коэффициент утонения дна заготовки: =.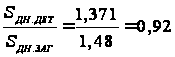