Реферат: Анализ сигналов и их прохождения через электрические цепи

Z1 - L последовательно C параллельно R₁ ,

Z2 - R.

С=20000 пФ, L=1.5 мкГн, R₁ =10⁴ R.

Добротность колебательной системы равна 50, резонансная частота контура совпадает с частотой радиоимпульса.

2.4 Условия

Дополнительные условия отсутствуют.

2.5 Срок выдачи задания курсовую работу

_______________________________________________

2.6 Срок выполнения курсовой работы

_______________________________________________

Задание выдал Задание получил

______________________ ________________________

______________________ ________________________

______________________ ________________________

2 АНАЛИЗ ФОРМЫ СИГНАЛА

2.1 Математическая модель видеосигнала и его спектр

Выражение для определения полиномов Чебышева (третьего рода) и полином Чебышева третьего порядка представлены формулами (2.1.1) и (2.1.2) соответственно.

T₃ (x) = (4*x³ -3*x)

Математическая модель видеосигнала представляет собой промасштабированный полином Чебышева третьего порядка. Масштабирование осуществляется путем замены переменной x на новую переменную kt. Коэффициент k выбирается так, чтобы выполнялось условие kt=1 при t=T и kt=-1 при t=-T (так как функция Чебышева ортогональна при -1<x<1). Параметр Т задан и , значит k=1/T.

После масштабирования полином Чебышева примет вид, представленный в формуле (2.1.3).

T₃ (x) = 4*(t/T)³ -3*(t/T)

Математическая модель видеосигнала будет описываться функцией, представленной в формуле (2.1.4) на промежутке tÎ[-T, T]. Окончательная модель видеосигнала имеет вид:

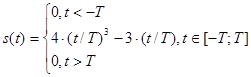
Так как большинство расчётов будет производиться преимущественно численными методами с помощью специализированного программного обеспечения, то математическую модель видеосигнала можно записать с помощью единичной функции. Это приведено в формуле (2.1.5).

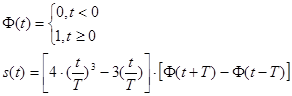
Графическое изображение модели видеосигнала приведено в приложении А на рисунке А.1

Спектральную плотность видеосигнала находится с помощью прямого преобразования Фурье математической модели видеосигнала:

где - оператор Фурье;

- спектральная плотность видеосигнала, ;

- частота, .

Спектральная плотность видеосигнала находится по формуле (2.1.7).

Графики спектральной плотности для заданного видеосигнала изображён в приложении А на рисунке А.2

2.2 Математические модели сигналов, соответствующих заданному видео сигналу, и их спектры

2.2.1 Периодическая последовательность видеосигналов

Математическая модель периодической последовательности видеосигналов, изображенная в приложении А на рисунке А.3, вычисляется по формуле (2.2.1.1)

где S_p (t) - математическая модель периодической последовательности видеосигналов;

s(t) – математическая модель видеосигнала;

- период повторения видеосигналов.