Реферат: Анализ сигналов и их прохождения через электрические цепи
где
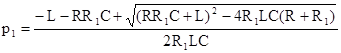, (5.19)
. (5.20)
Импульсная характеристика колебательного звена определяется преобразованием Лапласа от операторной передаточной функции.
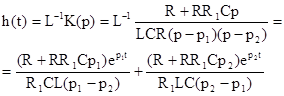(5.21)
Графические изображения импульсной и переходной характеристик колебательного звена приведены в приложении В на рисунках В.3 и В.4
4 АНАЛИЗ ПРОХОЖДЕНИЯ СИГНАЛОВ ЧЕРЕЗ ЦЕПИ
Анализ прохождения сигнала через апериодическое и колебательное звено будет производиться при помощи спектрального метода. Суть этого метода заключается в том, что если известен спектр сигнала на входе цепи и известен комплексный коэффициент передачи, то можно легко определить спектр сигнала на выходе цепи по формуле (4.1).
|
|
После того как получен спектр сигнала на выходе, надо выполнить обратное преобразование Фурье (формула (4.2)) и в результате получится сигнал на выходе.
4.4 Прохождение видеосигнала через апериодическое и колебательное звено
Графические изображения сигналов на выходе апериодического и колебательного звена при действии на вход видеосигнала приведены в приложении Г на рисунках Г.1 и Г.3
4.5 Прохождение радиосигнала через апериодическое и колебательное звено
Графические изображения сигналов на выходе апериодического и колебательного звена при действии на вход радиосигнала приведены в приложении Г на рисунках Г.2 и Г.4
5 АНАЛИЗ ПРОХОЖДЕНИЯ СЛУЧАЙНОГО СИГНАЛА ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ
|
где 
- энергетический спектр белого шума на входе;
|
|
- ???????.
|
где 
- энергетический спектр белого шума на выходе.
Автокорреляция сигнала определяется по формуле (5.3).
|
Интеграл 5.3 не берётся в элементарных функциях, поэтому будем его считать в дискретном виде через обратное дискретное преобразование Фурье.
5.1 Анализ прохождения случайного сигнала через апериодическое звено
Энергетический спектр сигнала на выходе апериодического звена определяется по формуле (5.1.1).
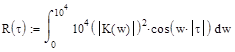
, где K(w)- комплексный коэффициент передачи апериодического звена.
В итоге, график корреляционной функции апериодического звена изображён в приложении Д на рисунке Д.1
5.2 Анализ прохождения случайного сигнала через колебательное звено
Энергетический спектр сигнала на выходе колебательного звена приведён формуле (5.2.1).
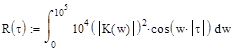
, где K(w)- комплексный коэффициент передачи колебательного звена.
В итоге, график корреляционной функции колебательного звена изображён в приложении Д на рисунке Д.2
Энергетический спектр белого шума на входе цепи постоянен, и определяется формулой (5.1), а спектр белого шума на выходе – формулой (5.2).
где - энергетический спектр белого шума на входе;
- частота.
|
|
|
где - энергетический спектр белого шума на выходе.
|
Интеграл 5.3 не берётся в элементарных функциях, поэтому будем его считать в дискретном виде через обратное дискретное преобразование Фурье.
|
В данной работе проводился анализ сигналов, спектров, характеристик электрических цепей. Оказалось, что, чем меньше длительность сигнала и чем больше его математическая модель имеет резких перепадов, тем шире получается его спектральная плотность. Дискретизация сигнала позволяет ограничить ширину спектра, но вносит искажения в форму сигнала при его восстановлении. При вычислении спектров сигналов и расчете прохождения сигналов через цепи, оказалось, достаточно удобно вычислять прямое и обратное преобразование Фурье при помощи численных методов, так как аналитическое выражение получается только для относительно простых сигналов и цепей.
7 СПИСОК ЛИТЕРАТУРЫ
7.1 Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 1988 - стр.
7.2 Баскаков С.И. Радиотехнические цепи и сигналы. Руководство к решению задач. – М.: Высшая школа, 1987 - стр.