Реферат: Быстрое преобразование Фурье
![]() (4).
(4).
Доказательство :
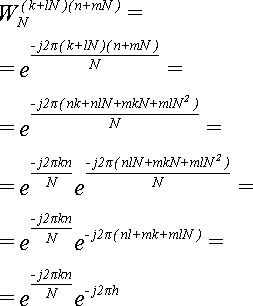 (5)
(5)
Величина -h = -(nl+mk+mlN) - целая, так как все множители целые, и все слагаемые целые. Значит, мы можем применить Теорему 0:
![]()
Что и требовалось доказать по (4).
Теорема 2 .
Для величины ![]() справедлива формула:
справедлива формула:
![]()
Доказательство :
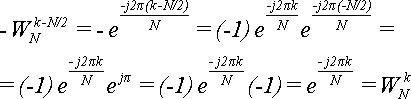
Алгоритм быстрого преобразования Фурье (БПФ) - это оптимизированный по скорости способ вычисления ДПФ. Основная идея заключается в двух пунктах.
- Необходимо разделить сумму (1) из N слагаемых на две суммы по N/2 слагаемых, и вычислить их по отдельности. Для вычисления каждой из подсумм, надо их тоже разделить на две и т.д.
- Необходимо повторно использовать уже вычисленные слагаемые.
Применяют либо "прореживание по времени" (когда в первую сумму попадают слагаемые с четными номерами, а во вторую - с нечетными), либо "прореживание по частоте" (когда в первую сумму попадают первые N/2 слагаемых, а во вторую - остальные). Оба варианта равноценны. В силу специфики алгоритма приходится применять только N, являющиеся степенями 2. Рассмотрим случай прореживания по времени.
Теорема 3 .
Определим еще две последовательности: {x[even] } и {x[odd] } через последовательность {x} следующим образом:
x[even]n = x2n ,
x[odd]n = x2n+1 , (6)
n = 0, 1,..., N/2-1
Пусть к этим последовательностям применены ДПФ и получены результаты в виде двух новых последовательностей {X[even] } и {X[odd] } по N/2 элементов в каждой.
Утверждается, что элементы последовательности {X} можно выразить через элементы последовательностей {X[even] } и {X[odd] } по формуле:
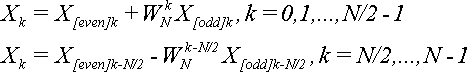 (7).
(7).
Доказательство :
Начинаем от формулы (2), в которую подставляем равенства из (6):
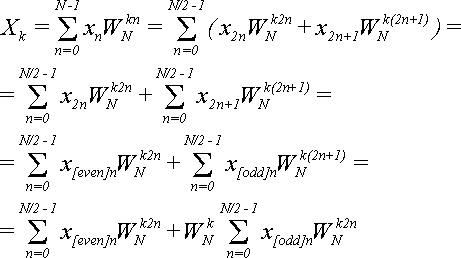 (8)
(8)
Теперь обратим внимание на то, что:
![]() (9)
(9)
Подставляя (9) в (8) получаем:
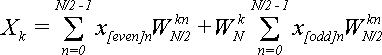 (10)
(10)
Сравним с формулами для X[even]k и X[odd]k при k = 0,1,…,N/2-1:
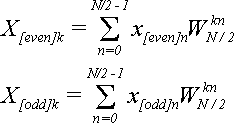 (11)
(11)
Подставляя (11) в (10) получим первую часть формулы (7):