Реферат: Быстрое преобразование Фурье

x = Re cos(2πt/T) - Im sin(2πt / T) (20)

Re = A cos φ, Im = A sin φ

По величинам Re и Im можно однозначно восстановить амплитуду и фазу исходной гармоники:

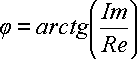и (21)

Рассмотрим очень распространенную практическую ситуацию. Пусть у нас есть звуковое или какое-то иное колебание в виде функции x = f(t). Пусть это колебание было записано в виде графика для отрезка времени [0, T]. Для обработки компьютером нужно выполнить дискретизацию . Отрезок делится на N-1 равных частей, границы частей обозначим t_n = nT/N. Сохраняются N значений функции на границах частей: x_n = f(t_n ) = { x₀ , x₁ , x₂ ,..., x_N }.

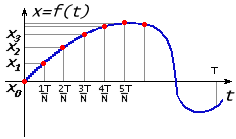
В результате прямого дискретного преобразования Фурье были получены N значений для X_k :

(22)

Теперь возьмем обратное преобразование Фурье:

(23)

Выполним над этой формулой следующие действия: разложим каждое комплексное X_k на мнимую и действительную составляющие X_k = Re_k + j Im_k ; разложим экспоненту по формуле Эйлера на синус и косинус действительного аргумента; перемножим; внесем 1/N под знак суммы и перегруппируем элементы в две суммы:

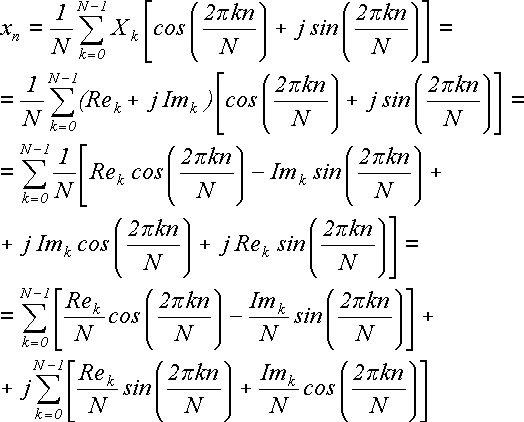(24)

Это была цепочка равенств, которая начиналась с действительного числа x_n . В конце получилось две суммы, одна из которых помножена на мнимую единицу j. Сами же суммы состоят из действительных слагаемых. Отсюда следует, что вторая сумма должна быть равна нулю. Отбросим ее и получим:

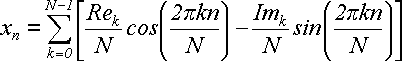(25)

Поскольку при дискретизации мы брали t_n = nT/N и , то можем выполнить замену: n = t_n N/T. Следовательно, в синусе и косинусе вместо 2πkn/N можно написать 2πkt_n /T. В результате получим:

(26)

Сопоставим эту формулу с формулой (20) для гармоники:

x = Re cos(2πt/T) - Im sin(2πt / T) (20)

Слагаемые суммы (26) аналогичны формуле (20), а формула (20) описывает гармоническое колебание. Значит сумма (26) представляет собой сумму из N гармонических колебаний разной частоты, фазы и амплитуды.

Выше объяснялось, каким образом формула вида (20) может быть преобразована в формулу вида (18):

x = A cos(2πt/T + φ) (18)

Выполним такое же преобразование для слагаемых суммы (26), преобразуем их из вида (20) в вид (18). Получим:

(27)

Далее будем функцию

G_k (t) = A_k cos(2πtk/T + φ_k ) (28)

называть k-й гармоникой .

Для вычисления A_k и φ_k надо использовать формулу (21). Теперь выпишем в одном месте все формулы, которые связывают амплитуду, фазу, частоту и период каждой из гармоник с коэффициентами X_k :

(29)

Итак.