Реферат: Быстрое преобразование Фурье
Данный алгоритм имеет тот недостаток, что требует разного числа вложенных циклов в зависимости от T. На практике это не очень плохо, поскольку T обычно ограничено некоторым разумным пределом (16..20), так что можно написать столько вариантов алгоритма, сколько нужно. Тем не менее, это делает программу громоздкой. Ниже я предлагаю вариант этого алгоритма, который эмулирует вложенные циклы через стеки Index и Mask.
int Index[MAX_T];int Mask[MAX_T];int R;for(I = 0; I < T; I++){ Index[I] = 0; Mask[I] = 1 << (T - I - 1);}J = 0;for(I = 0; I < N; I++){ if (I < J){ S = x[I]; x[I] = x[J]; x[J] = S; // ???????????? ????????? xI ? xJ} for(R = 0; R < T; R++) { J ^= Mask[R]; if (Index[R] ^= 1) // ???????????? Index[R] ^= 1; if (Index[R] != 0)break; }}Величина MAX_T определяет максимальное значение для T и в наихудшем случае равна разрядности целочисленных переменных ЭВМ. Этот алгоритм, может быть, чуть медленнее, чем предыдущий, но дает экономию по объему кода.
И, наконец, последний алгоритм. Он использует классический подход к многоразрядным битовым операциям: надо разделить 32-бита на 4 байта, выполнить перестановку в каждом из них, после чего переставить сами байты.
Перестановку бит в одном байте уже можно делать по таблице. Для нее нужно заранее приготовить массив reverse256 из 256 элементов. Этот массив будет содержать 8-битовые числа. Записываем туда числа от 0 до 255 и переставляем в каждом порядок битов.
Теперь этот массив применим для последней реализации функции reverse:
unsigned int reverse(unsigned int I, int T){ unsigned int R; unsigned char *Ic = (unsigned char*) &I; unsigned char *Rc = (unsigned char*) &R; Rc[0] = reverse256[Ic[3]]; Rc[1] = reverse256[Ic[2]]; Rc[2] = reverse256[Ic[1]]; Rc[3] = reverse256[Ic[0]];R >>= (32 - T); Return R;}Обращения к массиву reverse256 переставляют в обратном порядке биты в каждом байте. Указатели Ic и Ir позволяют обратиться к отдельным байтам 32-битных чисел I и R и переставить в обратном порядке байты. Сдвиг числа R вправо в конце алгоритма устраняет различия между перестановкой 32 бит и перестановкой T бит. Ниже приводится наглядная геометрическая иллюстрация алгоритма, где стрелками показаны перестановки битов, байтов и сдвиг.
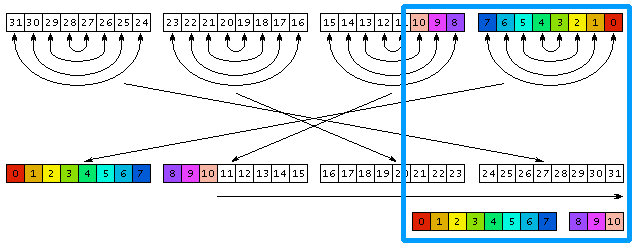
рис. 3
Оценим сложность описанных алгоритмов. Понятно, что все они пропорциональны N с каким-то коэффициентом. Точное значение коэффициента зависит от конкретной ЭВМ. Во всех случаях мы имеем N перестановок со сравнением I и J, которое предотвращает повторную перестановку некоторых элементов. Рядом присутствует некоторый обрамляющий код, применяющий достаточно быстрые операции над целыми числами: присваивания, сравнения, индексации, битовые операциии и условные переходы. Среди них в архитектуре Intel наиболее накладны переходы. Поэтому я бы рекомендовал последний алгоритм. Он содержит всего N переходов, а не 2N как в алгоритме со вложенными циклами или их эмуляцией и не NT как в самом первом алгоритме.
С другой стороны, предварительная перестановка занимает мало времени по сравнению с последующими операциями, использующими (N/2)log2 N умножений комплексных чисел. В таком случае тоже есть смысл выбрать не самый короткий, но самый простой и наглядный алгоритм - последний описанный. Вот его окончательный вид с небольшой оптимизацией:
static unsigned char reverse256[]= { 0x00, 0x80, 0x40, 0xC0, 0x20, 0xA0, 0x60, 0xE0,0x10, 0x90, 0x50, 0xD0, 0x30, 0xB0, 0x70, 0xF0,0x08, 0x88, 0x48, 0xC8, 0x28, 0xA8, 0x68, 0xE8, 0x18, 0x98, 0x58, 0xD8, 0x38, 0xB8, 0x78, 0xF8, 0x04, 0x84, 0x44, 0xC4, 0x24, 0xA4, 0x64, 0xE4, 0x14, 0x94, 0x54, 0xD4, 0x34, 0xB4, 0x74, 0xF4, 0x0C, 0x8C, 0x4C, 0xCC, 0x2C, 0xAC, 0x6C, 0xEC,0x1C, 0x9C, 0x5C, 0xDC, 0x3C, 0xBC, 0x7C, 0xFC,0x02, 0x82, 0x42, 0xC2, 0x22, 0xA2, 0x62, 0xE2, 0x12, 0x92, 0x52, 0xD2, 0x32, 0xB2, 0x72, 0xF2, 0x0A, 0x8A, 0x4A, 0xCA, 0x2A, 0xAA, 0x6A, 0xEA, 0x1A, 0x9A, 0x5A, 0xDA, 0x3A, 0xBA, 0x7A, 0xFA, 0x06, 0x86, 0x46, 0xC6, 0x26, 0xA6, 0x66, 0xE6, 0x16, 0x96, 0x56, 0xD6, 0x36, 0xB6, 0x76, 0xF6, 0x0E, 0x8E, 0x4E, 0xCE, 0x2E, 0xAE, 0x6E, 0xEE, 0x1E, 0x9E, 0x5E, 0xDE, 0x3E, 0xBE, 0x7E, 0xFE, 0x01, 0x81, 0x41, 0xC1, 0x21, 0xA1, 0x61, 0xE1,0x11, 0x91, 0x51, 0xD1, 0x31, 0xB1, 0x71, 0xF1,0x09, 0x89, 0x49, 0xC9, 0x29, 0xA9, 0x69, 0xE9, 0x19, 0x99, 0x59, 0xD9, 0x39, 0xB9, 0x79, 0xF9, 0x05, 0x85, 0x45, 0xC5, 0x25, 0xA5, 0x65, 0xE5, 0x15, 0x95, 0x55, 0xD5, 0x35, 0xB5, 0x75, 0xF5, 0x0D, 0x8D, 0x4D, 0xCD, 0x2D, 0xAD, 0x6D, 0xED, 0x1D, 0x9D, 0x5D, 0xDD, 0x3D, 0xBD, 0x7D, 0xFD, 0x03, 0x83, 0x43, 0xC3, 0x23, 0xA3, 0x63, 0xE3,0x13, 0x93, 0x53, 0xD3, 0x33, 0xB3, 0x73, 0xF3,0x0B, 0x8B, 0x4B, 0xCB, 0x2B, 0xAB, 0x6B, 0xEB, 0x1B, 0x9B, 0x5B, 0xDB, 0x3B, 0xBB, 0x7B, 0xFB, 0x07, 0x87, 0x47, 0xC7, 0x27, 0xA7, 0x67, 0xE7, 0x17, 0x97, 0x57, 0xD7, 0x37, 0xB7, 0x77, 0xF7, 0x0F, 0x8F, 0x4F, 0xCF, 0x2F, 0xAF, 0x6F, 0xEF, 0x1F, 0x9F, 0x5F, 0xDF, 0x3F, 0xBF, 0x7F, 0xFF,};unsigned int I, J;unsigned char *Ic = (unsigned char*) &I;unsigned char *Jc = (unsigned char*) &J;for(I = 1; I < N - 1; I++){ Jc[0] = reverse256[Ic[3]]; Jc[1] = reverse256[Ic[2]]; Jc[2] = reverse256[Ic[1]]; Jc[3] = reverse256[Ic[0]]; J >>= (32 - T); if (I < J) { S = x[I]; x[I] = x[J];x[J] = S; }}Напомним основные формулы:
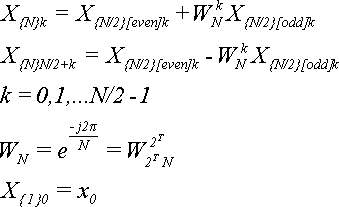 (16)
(16)
На рисунке проиллюстрирован второй этап вычисления ДПФ. Линиями сверху вниз показано использование элементов для вычисления значений новых элментов. Очень удобно то, что два элемента на определенных позициях в массиве дают два элемента на тех же местах. Только принадлежать они будут уже другим, более длинным массивам, размещенным на месте прежних, более коротких. Это позволяет обойтись одним массивом данных для исходных данных, результата и хранения промежуточных результатов для всех T итераций.
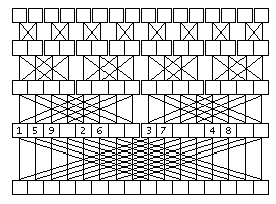
рис. 4
Итак, вот действия, которые нужно выполнить после первичной перестановки элементов.
#define T 4#define Nmax (2 << T)complex Q, Temp, j(0,1);static complex x[Nmax];static double pi2 = 2 * 3.1415926535897932384626433832795;int N, Nd2, k, mpNd2, m;for(N = 2, Nd2 = 1; N <= Nmax; Nd2 = N, N += N){ for(k = 0; k < Nd2; k++) { W = exp(-j*pi2*k/N); for(m = k; m < Nmax; m += N) { mpNd2 = m + Nd2; Temp = W * x[mpNd2]; x[mpNd2] = x[m] - Temp;x[m] = x[m] + Temp; } }}Переменная Nmax содержит полную длину массива данных и окончательное количество элементов ДПФ. В таблице показано соответствие между выражениями в формуле (16) и переменными в программе.
| В алгоритме | В формуле |
| N | N |
| Nd2 | N/2 |
| k | k |
| m | k с поправкой на номер последовательности |
| mpNd2 | k+N/2 с поправкой на номер последовательности |
| pi2 | 2π |
| j | j (мнимая единица) |
| x[k] (в начале цикла) | X{N/2}[even]k |
| x[mpNd2] (в начале цикла) | X{N/2}[odd]k |
| x[k] (в конце цикла) | X{N}k |
| x[mpNd2] (в конце цикла) | X{N}N/2+k |
| W |
Внешний цикл - это основные итерации. На каждой из них 2Nmax/N ДПФ (длиной по N/2 элементов каждое) преобразуются в Nmax/N ДПФ (длиной по N элементов каждое).
Следующий цикл по k представляет собой цикл синхронного вычисления элементов с индексами k и k + N/2 во всех результирующих ДПФ.
Самый внутренний цикл перебирает Nmax/N штук ДПФ одно за другим.
Именно так, а не иначе: сначала вычисляются элементы с номерами 0 и N/2, во всех ДПФ в количестве Nmax/N штук, потом с номерами 1 и N/2 + 1 и так далее. На рис.4 показана последовательность вычислений для N = 8. Такая последовательность обеспечивает однократное вычисление ![]() .
.
Обратите внимание, что x[mpNd2] вычисляется раньше, чем x[k], чтобы значение x[k] не было модифицировано прежде, чем будет использовано.
Алгоритм обратного дискретного преобразования Фурье отличается только тем, что вместо -j надо использовать +j и после всех вычислений поделить каждое x[k] на Nmax.
Для справки: произведение, сумма и экспонента для комплексных чисел вычисляются по формулам:
(x,y)(x',y')=(xx'-yy')(xy'+x'y)
(x,y)+(x',y')=(x+x')(y+y')
e-jv =(cos v, - sinv)
где v - действительное число.
В приведенной выше программе велико искушение для вычисления поворачивающих множителей использовать формулу:
![]() . (17)
. (17)
Это позволило бы избавиться от возведений в степень и обойтись одними умножениями, если заранее вычислить WN для N = 2, 4, 8,…, Nmax. Но то, что можно делать в математике, далеко не всегда можно делать в программах. По мере увеличения k поворачивающий множитель будет изменяться, но вместе с тем будет расти погрешность . Ведь вычисления с плавающей точкой на реальном компьютере совсем без погрешностей невозможны. И после N/2 подряд умножений в поворачивающем множителе может накопиться огромное отклонение от точного значения. Вспомним правило: при умножении величин их относительные погрешности складываются. Так что, если погрешность одного умношения равна s%, то после 1000 умножений она может достигнуть в худшем случае 1000s%.
Этого можно было бы избежать, будь число WN целым, но оно не целое при N > 2, так как вычисляется через синус и косинус:
![]()