Реферат: Быстрое преобразование Фурье

Это будет верно при k = 0,1,…,N/2-1.

Согласно теореме 1:

(12)

Подставим (12) в (10), и заменим по теореме 2:

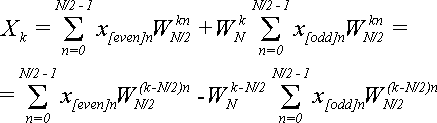(13)

Для k = N/2,…,N-1 по формуле (2):

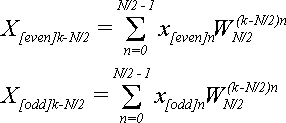(14)

Подставляем (14) в (13):

Эта формула верна для k = N/2,…,N-1 и, соответственно, (k - N/2) = 0,1,…,N/2-1 и представляет собой вторую и последнюю часть утверждения (7), которое надо было доказать.

Формула (7) позволяет сократить число умножений вдвое (не считая умножений при вычислении X_[even]k и X _[odd]k ), если вычислять X_k не последовательно от 0 до N - 1, а попарно: X₀ и X_N/2 , X₁ и X_N/2+1 ,..., X_N/2-1 и X_N . Пары образуются по принципу: X_k и X_N/2+k .

Теорема 4 .

ДПФ можно вычислить также по формуле:

(15)

Доказательство :

Согласно второй части формулы (7), получим:

Это доказывает второе равенство в утверждении теоремы, а первое уже доказано в теореме 3.

Также по этой теореме видно, что отпадает необходимость хранить вычисленные X_[even]k и X_[odd]k после использования при вычислении очередной пары и одно вычисление можно использовать для вычисления двух элементов последовательности {X}.

На этом шаге будет выполнено N/2 умножений комплексных чисел. Если мы применим ту же схему для вычисления последовательностей {X_[even] } и {X_[odd] }, то каждая из них потребует N/4 умножений, итого еще N/2. Продолжая далее в том же духе log₂ N раз, дойдем до сумм, состоящих всего из одного слагаемого, так что общее количество умножений окажется равно (N/2)log₂ N, что явно лучше, чем N² умножений по формуле (2).

Рассмотрим БПФ для разных N. Для ясности добавим еще один нижний индекс, который будет указывать общее количество элементов последовательности, к которой этот элемент принадлежит. То есть X_{R}k - это k-й элемент последовательности {X_{R} } из R элементов. X_{R}[even]k - это k-й элемент последовательности {X_{R}[even] } из R элементов, вычисленный по четным элементам последовательности {X_{2R} }. X_{R}[odd]k - это k-й элемент последовательности {X_{R}[odd] }, вычисленный по нечетным элементам последовательности {X_{2R} }.

В вырожденном случае, когда слагаемое всего одно (N = 1) формула (1) упрощается до:

,

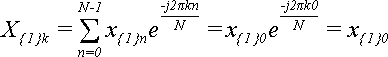Поскольку в данном случае k может быть равно только 0, то X_{1}0 = x_{1}0 , то есть, ДПФ над одним числом дает это же самое число.

Для N = 2 по теореме 4 получим:

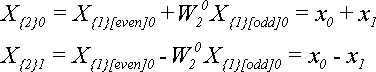
Для N = 4 по теореме 4 получим:

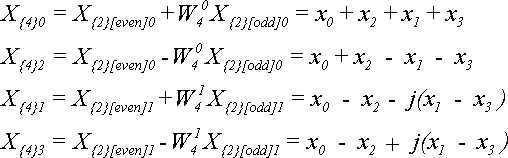
Отсюда видно, что если элементы исходной последовательности были действительными, то при увеличении N элементы ДПФ становятся комплексными.