Реферат: Численные методы 6
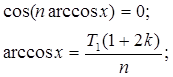
Так как arccosxÎ[0; Π];k=0,1,…n-1,чтобы туда попадал arcos
5. Корни многочлена Чебышева перемножаются, чередуются с точками их экстремума, причем максимум
Tn (x) на [-1;1] равен 1,т.е
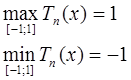
Для точек экстремума существует связь:
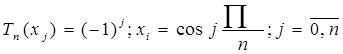
Введем нормированный многочлена Чебышева (старший коэффициент =1, перед х в максимальной степени)
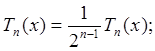(9.3)
Теорема Чебышева
Из всех многочленов степени n со старшим коэффициентом = 1, нормированный многочлен Чебышева отклоняется от нуля на отрезке [-1;1] , т.е не существует многочлена Рn *(x), что :
max | Рn *(x)| < max | T^n (x)|
[-1;1][-1;1] Доказательство не нужно.
Интерполяция по Чебышевским узлам
Задача: Пусть есть некоторая функция f(x), определенная на отрезке [a;b]. Как расположить на отрезке [a;b] n+1 узел интерполяции таким образом, чтобы минимизировать максимальное отклонение интерполяционного полинома Лагранжа от f(x), т.е ошибку аппроксимации.
Остаточный член полинома Лагранжа
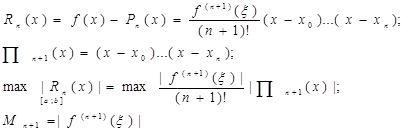
Необходимо минимизировать этот максимум, т.е необходимо найти такие узлы xk , 
которые минимизировали бы 
Сведем [a;b] к отрезку [-1;1]
Должна существовать связь хÎ[a;b] с tÎ[-1;1]
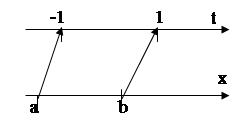
Связь: x= Ct+D
C-коэффициент сжатия (растяжения, D-параллельный перенос)
Если t=1
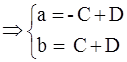
Если t=-1
Тогда:
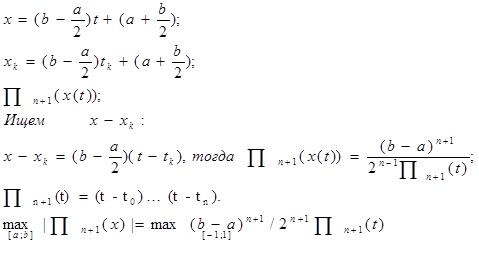(9.4)
Для того чтобы минимизировать (9.4), необходимо найти такие корни