Реферат: Численные методы 6

Если сплайн построен по некоторой таблично заданной функции f(x) таким образом, что S(х_i )= f(x_i ); x_i , i= - узлы интерполяции, то сплайн называют интерполяционным. Узлы сплайна и узлы интерполяции функции могут не совпадать.

Очевидно, что функция (10.1) является интерполяционным сплайном степени 1, дефекта 1, а кусочно-квадратичная функция (10.3) является интерполяционным сплайном, степени 2, дефекта 2.

Интерполяционный сплайн степени 3, дефекта 1.

Дважды непрерывно – дифференцируемый – сплайн.

Пусть задана табличная функция на [a;b], причем a= χ₀ ≤ χ₁ <…< χ_n =b (узлы сплайна совпадают с узлами интерполяции). Общий вид:

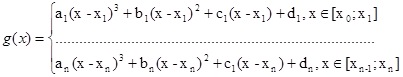
Условия:

1.) g(x_i ) = f(x_i )=y_i , i=

2.) g(x) = c² (дважды дифференцируема) [a;b]

3.) – краевые условия

Для нахождения неизвестных коэффициентов введем функцию

g_n (x) = a_k (x-x_k )³ + b_k (x-x_k )² +c₁ (x-x_k )+d_k , xÎ[ x_{k -1} ;x_k ]

1.) g₁ (x₀ ) = y₀ , g₁ (x₁ ) = y₁ , g₂ (x₂ ) = y₂ ,… g_n (x_n ) = y_n

2.) первое условие (сплайн интерполяционный)

3.)

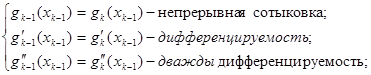
Краевые условия:

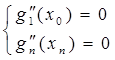
Таким образом, для нахождения 4n неизвестных мы построим 4n условий.

Теорема(10.1). Интерполяционный сплайн вида (10.5) для функции f(x) единственен.

Теорема(10.2). Пусть g(x)- интерполяционный сплайн степени 3 дефекта 1, построенный для функции f(x) С⁴ на отрезке [a;b], тогда для найдется такая константа C>0, что:

|f(x)- g(x)|<C⁴ , [a ;b],

= max(x_k -x_k-1 ), 1≤ k ≤ n

- максимальное расстояние между узлами интерполяции.

Линейный фильтр

Понятие линейного сплайна позволяет сформулировать подходы к построению линейных фильтров, предназначенных для устранения случайных ошибок в данных.

Обычно в ходе измерений на процесс фиксации данных оказывают влияние случайные помехи. Для того, чтобы уменьшить влияние этих помех на качество интерполяции осуществляют пересчет значений функции в узлах интерполяции по следующей формуле:

Квадратичный сплайн дефекта один

Узлы этого сплайна не совпадают с узлами интерполяции функции.