Реферат: Численные методы 6
Получим систему:
![]()
а0 x0 +b1 =y0 (решаем по отдельности каждую систему)
a2 x1 +b2 =y1
a2 x1 +b2 =y1
a2 x2 +b2 =y2 (10.2)
an xn-1 +bn =yn
an xn +bn = yn
Таким образом, получена система из 2n уравнений для поиска 2n неизвестных. Причем, система (10.2) образована из n систем линейных уравнений для 2-х неизвестных, каждая из которых может решаться независимо от остальных.
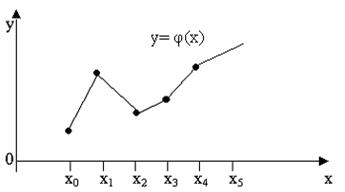
Кусочно-линейная функция φ(x) вида (10.1) внутри интервала (хi -1 ;xi ), ![]() непрерывна и дифференцируема, а в точках xi ,
непрерывна и дифференцируема, а в точках xi , ![]() непрерывна, но не дифференцируема(в этих точках к графику функции невозможно построить касательную).
непрерывна, но не дифференцируема(в этих точках к графику функции невозможно построить касательную).
Кусочно-квадратичная аппроксимация
Пусть f(x) задана таблично на [a;b], но n=2m (четно) a≤x0 <x1 <…<xn ≤b
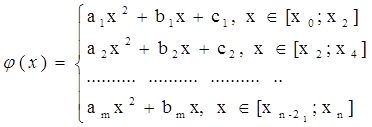
Чтобы функция приближала f(x) наложим ограничения φ(xi )=yi =f(xi ), ![]() .
.
Общее число узлов 2n+1, если n-четное.
Для нахождения неизвестных коэффициентов ak ,bk ,ck необходимо построить 3m условий.
k=1
[x0 ;x2 ]
Обобщим, получим систему:
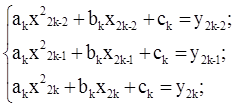
![]() (10.4)
(10.4)![]()
Для нахождения неизвестных имеем 3m условий. При каждом значении ![]() можем построить систему линейных уравнений для ak ,bk ,ck ;
можем построить систему линейных уравнений для ak ,bk ,ck ;
Решать ее можем независимо от остальных условий.
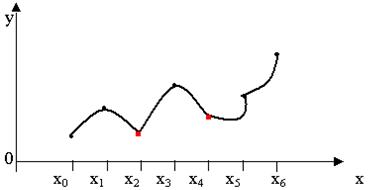
Кусочно- квадратичная φ(x) вида (10.3) внутри интервала (x2 n -2 -x2 n ), ![]() является непрерывной и дифференцируемой два раза, а в точках x2 i
является непрерывной и дифференцируемой два раза, а в точках x2 i ![]()
является непрерывной, но не дифференцируемой.
Определение Сплайна
Пусть на отрезке [a;b] задана некоторая система узлов a 0 ≤ x 0 < x 1 <…< xn ≤ b
Сплайном Sn ( x ) называется функция, которая определена на [a;b], l раз непрерывна и дифференцируема на нем, при этом на каждом из отрезков
[хк-1 ; хк ], к = ![]() , представляет собой многочлен степени m.
, представляет собой многочлен степени m.