Реферат: Численные методы 6

ЛЕКЦИЯ №9

МНОГОЧЛЕНЫ ЧЕБЫШЕВА

1. Определение и свойства

2. Интерполяция по Чебышевским узлам

3. Многочлены равномерных приближений

4. Экономизация степенных рядов

Многочленом Чебышева n-ой степени называется функция

T_n (x)=cos (narccos) n=0,1,2 …,xÎ[-1;1] ; (9.1)

Докажем, что при любом n=0,1,2

n=0: T₀ (x)=cos0=1;

n=1: T₁ (x)=cos(arccos x)=x;

n=2: T₂ (x) =cos(2arccos x);

Обозначимα=arccosx

T_n (x)=cos2α ;

T_n+1 (x)=cos((n+1)α) ;

T_n-1 (x)=cos((n-1)α) ;

cos((n+1)α)+ cos((n-1)α)-2cos(2nα/ α)cos(2α/ α)=2 cosnα cosα;

T_n+1 (x)+ T_n-1 (x)=2 T₁ (x) T_n (x);

T_n+1 (x)= 2xT_n (x)- T_n-1 (x); (9.2)

Свойства многочлена Чебышева:

1. Все функции T_n (x) являются многочленами при n=0,1,2,…

2. Степени этих многочленов возрастают с увеличением n, причем старший член T_n (x)=2^{n -1} x_n

3. Многочлены T_n (x) при четных n выражаются через четные функции , при нечетных n-через нечетные функции.

Проверим:

T₂ (x) =2х² -1

T₃ (x) =2х (2х² -1) =4х³ -2х

T₄ (x) = 2х (4х³ -3х)-2х² +1=2³ х⁴ -3х² +1

4. На отрезке [-1;1] многочлен T_n (x) имеет ровно n различных действительных корней, которые рассчитываются по формуле:

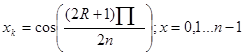
--> ЧИТАТЬ ПОЛНОСТЬЮ <--