Реферат: Численные методы 6

По теореме Чебышева полином Т_{n +1} нормирован многочленом Чебышева, наименее отклонен от нуля на [-1;1], поэтому в качестве искомых корней необходимо взять корни многочлена Чебышева на [-1;1]

(рассмотрим полином n+1-ой степени)

(9.5)

Узлы интерполяции, определим по формуле (9.5) обеспечивают min, max ошибку аппроксимации при помощи интерполяционных полиномов.

Многочлены равномерных приближений

Если функция f(x) ∞-но дифференцируема на [a;b] и в качестве узлов интерполяции берутся корни многочленов Чебышева, приведенные к [a;b], то справедливо:

Т.е имеет место равномерная сходимость последовательности интерполяционного полинома Лагранжа функции f(x).

Теорема Вейерштрасса : для любой непрерывной функции f(x) на [a;b] найдется полином Q_n (x), что |f(x)- Р_n (x)| < ξ для любой ξ>0 , любое хÎ[a;b].

Т.е для любой f(x) непрерывной на [a;b],может быть построена аппроксимирующий наилучший полином, который минимизирует максимальное отклонение между f(x) и Q_n (x). Такие полиномы называютмногочленами наилучших равномерных приближений.

К сожалению, общий вид таких полиномов и способы построения не известны.

Экономизация степенных рядов

Ряд Тейлора представляет собой локальную аппроксимацию для f(x) степенной функции вида xⁿ можно заменить многочлен Чебышева и получить разложение по этим многочленам вместо степенного ряда:

Такой процесс называется экономизацией степенного ряда.

Разложение по многочленам Чебышева имеет меньшую максимальную погрешность.

ЛЕКЦИЯ №10,11

ИНТЕРПОЛЯЦИОННЫЕ СПЛАЙНЫ

Когда интерполяционный отрезок [a;b] велик, нет, основания считать, функцию f(x) достаточно гладкой, на [a;b], то нельзя повышать точность аппроксимации за счет увеличения степени интерполяционного многочлена.

Связано это с тем, что у многочлена n-ой степени может быть n-1 точка экстремума. При n→∞ график многочлена начинает сильно колебаться

Такое явление называют феноменом Рунге.

Поэтому более перспективным является применение кусочно-полиномиальной аппроксимации, при которой аппроксимирующая функция составляется из отдельных многочленов (сплайнов). Каждый из которых (одинаковы и наибольшей степени) определен на своем участке отрезка [a;b].

Рассмотрим аппроксимацию кусочно-линейной функции (линейный сплайн).

Пусть f(x) задана таблично на [a;b], т. е определены некоторые узлы интерполяции a≤x₀ <x₁ <…<x_n ≤b

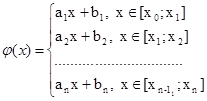кусочно-линейная функция

Необходимо: φ(x_i )=y_i =f(x_i ), для приближения функции.

Определим a_i и b_i .

x=x₀ : φ(x₀ )=f(x₀ )=y₀ a₁ x₀ +b₁ =y₀

x=x₁ : φ(x₁ )=f(x₁ )=y₁ a₁ x₁ +b₁ =y₁

a₂ x₁ +b₂ =y₁