Реферат: Числові характеристики системи випадкових величин та їх граничні теореми
 .
.

 .
.
Для опису зв'язків, що існують між проекціями випадкового вектора (x,h), крім коваріації ![]() можна використовувати числові характеристики умовних законів розподілу
можна використовувати числові характеристики умовних законів розподілу ![]() ,
, ![]() .
.
Умовним середнім значенням ![]() і умовною дисперсією
і умовною дисперсією ![]() випадкової величини x за умови h =y називаються величини:
випадкової величини x за умови h =y називаються величини:
 ,
,
 .
.
Аналогічно визначаються характеристики ![]() і
і ![]() .
.
Для опису випадкового вектора також вводять початкові і центральні моменти:
![]() ,
, ![]() .
.
2. Комплексна випадкова величина, характеристичні функції
Комплексна випадкова величина, що вводиться за формулою ![]() , є іншим способом опису випадкового вектора (
, є іншим способом опису випадкового вектора (![]() ,
,![]() ).
).
Випадкові величини ![]() і
і ![]() називаються незалежними, якщо незалежними є випадкові вектори (
називаються незалежними, якщо незалежними є випадкові вектори (![]() ,
,![]() ) і (
) і (![]() ,
,![]() ).
).
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Характеристичною функцією випадкової величини ![]() називається середнє значення виразу
називається середнє значення виразу ![]() .
.
![]() .
.
Функцію ![]() називають також характеристичною функцією відповідного закону розподілу:
називають також характеристичною функцією відповідного закону розподілу:
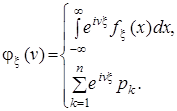 (2)
(2)
Як видно з (2), характеристична функція ![]() є перетворенням Фур'є відповідної їй щільності імовірності:
є перетворенням Фур'є відповідної їй щільності імовірності: