Реферат: Числові характеристики системи випадкових величин та їх граничні теореми

Рисунок 1

Внаслідок своєї загальності нерівність Чебишева дає дуже грубу оцінку ймовірності, що входить до неї.

Наприклад, .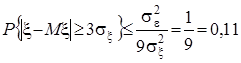

, якщо .

Вважають, щопослідовність функцій розподілу , , ,...., ,... збігається до функції розподілу , якщо

в усіх точках неперервності.

Якщо , то .

Практичне використання теорії ймовірностей засновано на такому принципі: випадкову подію, ймовірність якої досить близька до 1, можна вважати достовірною та неможливою при дуже малій ймовірності.

Теореми, що забезпечують виконання такої схеми обробки даних, називаються законами великих чисел.

Теорема Чебишева

Нехай h₁ , h₂ …–послідовність попарно незалежних випадкових величин, дисперсії яких обмежені

, k=1,2 …

Тоді при будь-якому e>0

.

Теорема Бернуллі.

Нехай x_n – число появ деякої події А в серії з n незалежних іспитів, р – ймовірність появи А в окремому іспиті.

Тоді

тобто для кожного e>0

Застосовуючи теорему Чебишева, одержимо формулу, що очікуємо при необмеженій кількості випробувань.

®р.

Збіг теоретичних розрахунків із закономірностями, що фактично спостерігаються, свідчить про правильну схему побудови теорії ймовірностей. збіжність випадковий величина ймовірність

Центральна гранична теорема.

Нехай x₁ ,x₂ ,…послідовність незалежних випадкових величин, що мають дисперсію D₁ ,D₂ ,…D_n …Треті абсолютні центральні моменти їх обмежені m_k =M|x_k -Mx_k |³ £C.

Тоді випадкова величина