Реферат: Диференціальні операції в скалярних і векторних полях. Основні поняття і формули
1. Скалярне поле
Нехай ![]() – область у тривимірному просторі (або на площині). Кажуть, що в області
– область у тривимірному просторі (або на площині). Кажуть, що в області ![]() задано скалярне поле, якщо кожній точці
задано скалярне поле, якщо кожній точці ![]() поставлено у відповідність деяке число
поставлено у відповідність деяке число ![]() .
.
Прикладами скалярних полів є поле температури даного тіла, поле густини даного неоднорідного середовища, поле вологості повітря, поле атмосферного тиску, поле потенціалів заданого електростатичного поля тощо.
Поверхня (лінія), на якій функція ![]() набуває одне й те саме значення, називається поверхнею (лінією) рівня скалярного поля (наприклад, поверхні або лінії постійної температури). Надаючи
набуває одне й те саме значення, називається поверхнею (лінією) рівня скалярного поля (наприклад, поверхні або лінії постійної температури). Надаючи ![]() різних постійних значень:
різних постійних значень: ![]() , отримаємо сім’ю поверхонь (ліній) рівня даного скалярного поля.
, отримаємо сім’ю поверхонь (ліній) рівня даного скалярного поля.
Фізичні скалярні поля не залежать від вибору системи координат: величина ![]() є функцією лише точки
є функцією лише точки ![]() і, можливо, часу (нестаціонарні поля).
і, можливо, часу (нестаціонарні поля).
Якщо в просторі ввести прямокутну систему координат ![]() , то точка
, то точка ![]() у цій системі координат матиме певні координати
у цій системі координат матиме певні координати ![]() і скалярне поле
і скалярне поле ![]() стане функцією цих координат:
стане функцією цих координат: ![]() .
.
2. Векторне поле
Кажуть, що в області ![]() задано векторне поле, якщо кожній точці
задано векторне поле, якщо кожній точці ![]() поставлено у відповідність деякий вектор
поставлено у відповідність деякий вектор ![]() .
.
Фізичні приклади векторних полів: електричне поле системи електричних зарядів, яке характеризується в кожній точці вектором напруженості ![]() ; магнітне поле, утворене електричним струмом і яке характеризується в кожній точці вектором магнітної індукції
; магнітне поле, утворене електричним струмом і яке характеризується в кожній точці вектором магнітної індукції ![]() ; поле тяжіння, утворене системою мас і яке характеризується в кожній точці вектором сили тяжіння
; поле тяжіння, утворене системою мас і яке характеризується в кожній точці вектором сили тяжіння ![]() , що діє в цій точці на одиничну масу; поле швидкостей потоку рідини, яке описується в кожній точці вектором швидкості
, що діє в цій точці на одиничну масу; поле швидкостей потоку рідини, яке описується в кожній точці вектором швидкості ![]() .
.
Зручною геометричною характеристикою векторногополя ![]() є векторні лінії – криві, в кожній точці
є векторні лінії – криві, в кожній точці ![]() яких вектор
яких вектор ![]() напрямлений по дотичній до кривої. Векторні лінії поля тяжіння, електричного і магнітного полів називається силовими лініями, а поля швидкостей – лініями струму.
напрямлений по дотичній до кривої. Векторні лінії поля тяжіння, електричного і магнітного полів називається силовими лініями, а поля швидкостей – лініями струму.
Нехай векторна лінія, яка проходить через точку ![]() , описується рівнянням
, описується рівнянням ![]() , де
, де ![]() – параметр. Умова колінеарності вектора поля
– параметр. Умова колінеарності вектора поля ![]() і дотичного вектора
і дотичного вектора ![]() в довільній точці цієї лінії має вигляд
в довільній точці цієї лінії має вигляд
![]() ,(1)
,(1)
де ![]() – деяке число. Умову (1) можна записати також у вигляді
– деяке число. Умову (1) можна записати також у вигляді
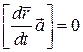 (2)
(2)
або, помноживши на ![]() , у вигляді
, у вигляді
![]() .(3)
.(3)
Кожне із рівнянь (1) – (3) є диференціальним рівнянням векторних ліній у векторній формі і визначає множину векторних ліній. Конкретна векторна лінія, яка проходить через задану точку ![]() , визначається додатковою умовою
, визначається додатковою умовою
![]() ,(4)
,(4)
де ![]() – радіус-вектор точки
– радіус-вектор точки ![]() .
.
Фізичні векторні поля не залежать від системи координат: в кожній точці ![]() вектор
вектор ![]() повністю визначається своїм модулем
повністю визначається своїм модулем ![]() і напрямом. Якщо в просторі введена прямокутна система координат
і напрямом. Якщо в просторі введена прямокутна система координат![]() , то векторне поле
, то векторне поле ![]() описується вектор-функцією трьох змінних
описується вектор-функцією трьох змінних ![]() або трьома скалярними функціями – її координатами:
або трьома скалярними функціями – її координатами:
![]() .
.
Оскільки в прямокутних координатах![]() , то векторне рівняння (3) для векторних ліній еквівалентне системі диференціальних рівнянь
, то векторне рівняння (3) для векторних ліній еквівалентне системі диференціальних рівнянь
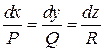 ,(5)
,(5)
а додаткове векторне рівняння (4) еквівалентне таким умовам:
![]() ,(6)
,(6)
де ![]() – координати точки
– координати точки![]() .
.
3. Похідна за напрямом
Скалярне і векторне поля
![]() і
і ![]()
--> ЧИТАТЬ ПОЛНОСТЬЮ <--