Реферат: Диференціальні операції в скалярних і векторних полях. Основні поняття і формули

диференційовані разів. Надалі розглядатимемо поля, диференційовані потрібне нам число разів.

Нехай – скалярне поле, задане в області , – одиничний фіксований вектор; – фіксована точка; – довільна точка із , відмінна від і така, що вектор колінеарний . Нехай, далі, – величина напрямленого відрізка (вона дорівнює його довжині 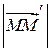, якщо напрям вектора збігається з напрямом вектора , і дорівнює – , якщо вектори 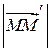і є протилежними).

Означення. Число називається похідною скалярного поля (функції) в точці за напрямом і позначається символом.

Похідна за напрямом є швидкістю зміни функції за напрямом в точці.

Якщо в прямокутній системі координат , то

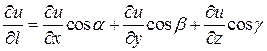.(7)

Зокрема, якщо вектор збігається з одним із ортів або , то похідна за напрямком збігається з відповідною частинною похідною. Наприклад, якщо , то

.

Аналогічно визначається похідна за напрямом векторного поля.

Означення . Вектор 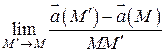називається похідною векторного поля (вектор-функції) в точці за напрямом і позначається символом.

Якщо в прямокутній системі координат , то

.

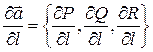4. Градієнт скалярного поля

скалярне векторне поле дивергенція

Означення . Градієнтом скалярного поля називається вектор-функція

.

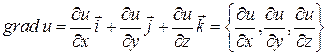Із рівності (7) випливає, що

,(8)

Звідси , оскільки .

Тут – кут між векторами і в точці. Очевидно, що має найбільше значення при, тобто у напрямі в даній точці. Інакше кажучи, вектор в даній точці вказує напрям найбільшого зростання поля (функції ) у цій точці, а є швидкість зростання функції в цьому напрямі. Таким чином, вектор не залежить від вибору системи координат, а його модуль і напрям у кожній точці визначається самою функцією.

5. Потенціальне поле

Означення. Векторне поле називається потенціальним в області, якщо воно збігається в області з полем градієнта деякого скалярного поля:

.(9)

Функція називається скалярним потенціалом векторного поля. Якщо, то із рівності (9) випливає, що

.

Інколи потенціалом векторного поля називають таку функцію , що .

Розглянемо, наприклад, поле тяжіння точкової маси , розміщеної на початку координат. Воно описується вектор-функцією ( – гравітаційна стала, ). З такою силою діє це поле на одиничну масу, розміщену в точці . Поле тяжіння є потенціальним. Його можна подати у вигляді градієнта скалярної функції , яка називається ньютонівським потенціалом поля тяжіння точкової маси . Дійсно

.