Реферат: Диференціальні операції в скалярних і векторних полях. Основні поняття і формули

.

Розглянемо потенціальне поле . Його потенціал . Обчислимо ротор цього поля:

.

Взагалі, ротор довільного потенціального поля дорівнює нулю (див. підрозділ 2). Тому кажуть, що потенціальне поле є безвихровим.

8. Соленоїдальне поле

Векторне поле називається соленоїдальним в області , якщо в цій області . Оскільки характеризує густину джерел поля, то в тій області, де поле соленоїдальне, немає джерел цього поля.

Наприклад, електричне поле точкового заряду соленоїдальне (задовольняє умову ) всюди поза точкою, де знаходиться заряд (в цій точці ). Векторні лінії соленоїдального поля не можуть починатися або закінчуватися на межі області, або бути замкненими кривими. Прикладом соленоїдального поля з замкненими векторними лініями є магнітне поле, яке створюється струмом у провіднику.

Якщо векторне поле можна подати як ротор деякого векторного поля , тобто , то вектор – функція називається векторним потенціалом поля .

Можна перевірити (див. докладніше п. 2), що , тобто поле є соленоїдальним.

Довільне векторне поле можна подати у вигляді суми потенціального і соленоїдального полів.

9. Оператор Гамільтона

Згадаємо, що символ називається оператором частинної похідної по . Під добутком цього оператора на функцію розумітимемо частинну похідну , тобто . Аналогічно, і – оператори частинних похідних по і по .

Введемо векторний оператор «набла» або оператор Гамільтона:

.

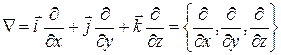За допомогою цього символічного (операторного) «вектора» зручно записувати і виконувати операції векторного аналізу.

У результаті множення вектора на скалярну функцію отримуємо :

.

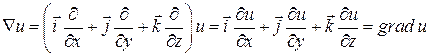Скалярний добуток вектора на вектор – функцію дає:

.

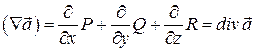Векторний добуток вектора на вектор – функцію дає:

.

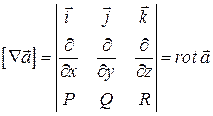10. Нестаціонарні поля

Нехай в області визначено нестаціонарне скалярне поле : величина є функцією точки і часу . Приклад такого поля – змінний з часом розподіл температури в будь-якому середовищі (наприклад, в потоці рідини). Розглянемо точку , яка рухається в області (частинку рідини). Координати точки (частинки) змінюються з часом за відомим законом . Величина в рухомій точці є складеною функцією :

.

Обчислимо похідну по цієї функції (вона називається повною похідною). За правилом диференціювання складеної функції знаходимо

.

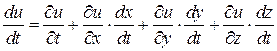Вводячи в точці вектор швидкості 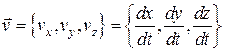, отримуємо

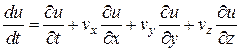
Або