Реферат: Дифференциальные уравнения I и II порядка

Пусть рассматривается дифференциальное уравнение первого порядка общего вида F(x,y,y^/ )=0.

Тогда существование его особого решения прежде всего может быть связано с условием , не обеспечивающим представление y^/ как неявной функции переменных x и y, задаваемой уравнением F(x,y,y^/ )=0.

Таким образом, формируя систему уравнений

,

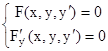и исключая из нее переменную y^/ , получаем функцию y=y(x), которая может дать особое решение дифференциального уравнения F(x,y,y^/ )=0.

Определение. Кривая, получаемая исключением параметра p из системы уравнений

,

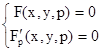называется дискретной кривой уравнения F(x,y,y^/ )=0.

Для того, чтобы дискретная кривая давала особое решение дифференциального уравнения, остается проверить, что она удовлетворяет уравнению F(x,y,y^/ )=0, и что через каждую ее точку проходит хотя бы одна интегральная кривая общего решения этого уравнения, т.е. проверить, что в точках дискретной кривой нарушается свойство единственности решения дифференциального уравнения.

Пример 1. Дано уравнение .

Как было указано выше его особое решение дается уравнениями y=x+c и y=-x+c. Опреляя для него дискретную кривую имеем систему уравнений

.

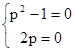Очевидно, данная система решения не имеет, поэтому рассматриваемое дифференциальное уравнение особых решений не имеет.

Пример 2. Рассмотрим решение уравнения

Его общее решение имеет вид . Выписывая систему уравнений

или , (где p=y^/ )

и исключая из нее переменную p, получаем уравнение дискретной кривой y=0 (ось Ox). Очевидно, она является решением дифференциального уравнения, так как из y=0=const следует y^/ =0. Кроме того через любую точку M(x₀ ;0) этой кривой проходит частное решение дифференциального уравнения, получаемое из общего при c=-x₀ . Не трудно убедиться, что касательные в точке M(x₀ ;0) дискретной кривой и частного решения совпадают. Таким образом, дискретная кривая y=0 является особым решением исходного дифференциального уравнения.

Ниже на рис. 3 изображено семейство интегральных кривых этого уравнения, являющееся семейством парабол.

Из рисунка видно, что дискретная кривая y=0, являющаяся осью Ox, касается в каждой точке некоторой кривой семейства.

Выше была рассмотрена ситуация, когда уравнение F(x,y,y^/ )=0 не определяло y^/ как неявную функцию переменных x и y, так как выполнялось условие .

Предположим теперь, что в области D, где ищется решение дифференциального уравнения, выполняется условие . В этом случае уравнение F(x,y,y^/ )=0 определяет y^/ как неявную функцию от x и y, т.е. можно считать y^/ =f(x,y) или даже явно выразить y^/ через x и y в виде y^/ =f(x,y). Тогда особое решение будет связано с нарушением условий приведенной выше в параграфе 3, теоремы Коши существования и единственности решения дифференциального уравнения.

Таким невыполнимым условием, обычно, берется условие Липшица, и геометрическое место точек, в которых оно нарушается, задается условием или, считая , условием .

Пример 3. Рассматривается дифференциальное уравнение (сравните с примером 2). Здесь . Так как , то дискретная кривая отсутствует. Из и условия , находим, что в точках кривой y=0, являющейся осью Ox, нарушается условие теоремы Коши. Следовательно, эта кривая y=0 может быть особым решением. Остается проверить, что она удовлетворяет исходному дифференциальному уравнению и что в ее точках нарушается условие единственности прохождения интегральной кривой. Общее решение данного уравнения имеет вид , т.е. такой же, как и в примере 2. Разбирая пример 2, выполнимость обоих условий была проверена. Следовательно, решение y=0 действительно является особым.

Пример 4. Дано уравнение .

Для него , т.е. дискретной кривой нет. Из и условия , получаем точки кривой y=0, в которых нарушены условия теоремы Коши.

Однако, в данном случае кривая y=0 не удовлетворяет дифференциальному уравнению. Следовательно, это уравнение особых решений не имеет.

Особым решением дифференциального уравнения довольно часто бывают огибающие семейства его интегральных кривых.

Определение. Кривая y=y(x) называется огибающей семейства интегральных кривых интегрального уравнения, задаваемого общим решением Ф(x,y,c)=0, если в каждой точке она касается одной из кривых данного семейства, т.е. имеет с ней в этой точке общую касательную.

Для нахождения огибающей может быть использован следующий подход.